高一（上）数学单元同步练习
第一单元 集合
[重点]
理解集合的概念，集合的性质，元素与集合的表示方法及其关系。
集合的子、交、并、补的意义及其运用。掌握有关术语和符号，准确使用集合语言表述、研究、处理相关数学问题。
[难点]
有关集合的各个概念的涵义以及这些概念相互之间的区别与联系。
准确理解、运用较多的新概念、新符号表示处理数学问题。
一、选择题
|
|
1．下列八个关系式①{0}=
②=0 ③ {} ④
{} ⑤{0}
⑥0
⑦
{0} ⑧{}其中正确的个数（ ）
（A）4 （B）5 （C）6 （D）7
2．集合{1，2，3}的真子集共有（ ）
（A）5个 （B）6个 （C）7个 （D）8个
3．集合A={x
} B={
} C={
}又
则有（ ）
（A）（a+b） A
(B) (a+b) B
(C)(a+b) C (D) (a+b) A、B、C任一个
4．设A、B是全集U的两个子集，且A
B，则下列式子成立的是（ ）
（A）CUACUB （B）CUA
CUB=U
（C）A
CUB=
（D）CUAB=
5．已知集合A={
} B={
}则A
=（ ）
（A）R
（B）{
}
（C）{
} （D）{
}
6．下列语句：（1）0与{0}表示同一个集合；（2）由1，2，3组成的集合可表示为{1，2，3}或{3，2，1}；（3）方程（x-1）2(x-2)2=0的所有解的集合可表示为{1，1，2}；（4）集合{
}是有限集，正确的是（ ）
（A）只有（1）和（4） （B）只有（2）和（3）
（C）只有（2） （D）以上语句都不对
7．已知A={1，2，a2-3a-1},B={1,3},A
{3,1}则a等于（ ）
（A）-4或1 （B）-1或4 （C）-1 （D）4
8.设U={0，1，2，3，4}，A={0，1，2，3}，B={2，3，4}，则（CUA）（CUB）=（ ）
（A）{0} （B）{0，1}
（C）{0，1，4} （D）{0，1，2，3，4}
9．设S、T是两个非空集合，且S
T，TS，令X=S
那么SX=（ ）
（A）X （B）T （C） （D）S
10．设A={x
},B={x
},若AB={2,3,5},A、B分别为（ ）
（A）{3，5}、{2，3} （B）{2，3}、{3，5}
（C）{2，5}、{3，5} （D）{3，5}、{2，5}
11．设一元二次方程ax2+bx+c=0(a<0)的根的判别式
，则不等式ax2+bx+c
0的解集为（ ）
（A）R
（B）
（C）{
} （D）{
}
|
（C）P=Q （D）P |
12．已知P={
}，Q={
，对于一切
R成立}，则下列关系式中成立的是（ ）
13．若M={
}，N={
Z}，则MN等于（ ）
（A）
（B）{} （C）{0}
（D）Z
14．下列各式中，正确的是（ ）
（A）2
（B）{
}
（C）{
}
（D）{
}={
}
15．设U={1，2，3，4，5}，A，B为U的子集，若AB={2}，（CUA）B={4}，（CUA）（CUB）={1，5}，则下列结论正确的是（ ）
（A）3
（B）3
（C）3
（D）3
16．若U、分别表示全集和空集，且（CUA）
A，则集合A与B必须满足（ ）
(A)
(B)
(C)B=
(D)A=U且AB
17．已知U=N，A={
}，则CUA等于（ ）
（A）{0，1，2，3，4，5，6} （B）{1，2，3，4，5，6}
（C）{0，1，2，3，4，5} （D）{1，2，3，4，5}
18．二次函数y=-3x2+mx+m+1的图像与x轴没有交点，则m的取值范围是（ ）
（A）{
} （B）{
}
（C）{
} （D）{
}
19．设全集U={（x,y）
},集合M={（x,y）
}，N={(x,y)
},那么（CUM）（CUN）等于（ ）
（A）{（2，-2）} （B）{（-2，2）}
（C）
（D）（CUN）
20．不等式
<x2-4的解集是（ ）
（A）{x
}
（B）{x
}
（C）{ x
}
（D）{ x
}
二、填空题
1． 在直角坐标系中，坐标轴上的点的集合可表示为
2． 若A={1,4,x},B={1,x2}且AB=B，则x=
3． 若A={x
} B={x
},全集U=R，则A
=
4． 若方程8x2+(k+1)x+k-7=0有两个负根，则k的取值范围是
5． 集合{a,b,c}的所有子集是 真子集是 ；非空真子集是
6． 方程x2-5x+6=0的解集可表示为
方程组
7．设集合A={
},B={x
},且AB，则实数k的取值范围是
。
8．设全集U={x
为小于20的非负奇数}，若A（CUB）={3，7，15}，（CUA）B={13，17，19}，又（CUA）（CUB）=，则AB=
9．设U={三角形}，M={直角三角形}，N={等腰三角形}，则MN=
MN=
CUM=
CUN=
CU（MN）=
10．设全集为，用集合A、B、C的交、并、补集符号表图中的阴影部分。
（1） （2）
 |
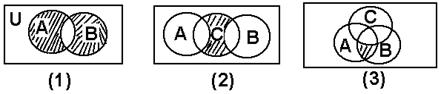（3）
三、解答题
1．设全集U={1，2，3，4}，且={
x2-5x+m=0,xU}若CUA={1，4}，求m的值。
2．已知集合A={a关于x的方程x2-ax+1=0,有实根}，B={a不等式ax2-x+1>0对一切xR成立},求AB。
3．已知集合A={a2,a+1,-3},B={a-3,2a-1,a2+1},若AB={-3}，求实数a。
4．已知方程x2-(k2-9)+k2-5k+6=0的一根小于1，另一根大于2，求实数k的取值范围。
5．设A={x
,其中xR,如果AB=B，求实数a的取值范围。
6．设全集U={x
},集合A={x
},B={x2+px+12=0},且（CUA）B={1，4，3，5}，求实数P、q的值。
7．若不等式x2-ax+b<0的解集是{
}，求不等式bx2-ax+1>0的解集。
8．集合A={（x,y）
},集合B={（x,y）
,且0
}，又A
，求实数m的取值范围。
第一单元 集合
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | B | C | B | C | B | C | D | A |
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 | D | A | A | D | C | D | A | D | A | B |
二、填空题答案
1．{(x,y)
} 2.0,
3.{x
,或x3}
4.{
} 5.,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c};除去{a,b,c}外所有子集；除去及{a,b,c}外的所有子集
6.{2,3};{2,3}
7.{
}
8.{1,5,9,11} 9.{等腰直角三角形}；{等腰或直角三角形}，{斜三角形}，{不等边三角形}，{既非等腰也非直角三角形}。 10.（1） （AB）
（2）[（CUA）（CUB）]
；（3）（AB）（CUC）
三、解答题
1．m=2×3=6 2.{a
}
3.a=-1
4. 提示：令f(1)<0 且f(2)<0解得
5．提示：A={0，-4}，又AB=B，所以BA
（Ⅰ）B=时，
4（a+1）2-4(a2-1)<0，得a<-1
(Ⅱ)B={0}或B={-4}时，0 得a=-1
（Ⅲ）B={0，-4}，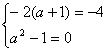
解得a=1
综上所述实数a=1 或a
-1
6．U={1，2，3，4，5} A={1，4}或A={2，3}
CuA={2,3,5}或{1，4，5} B={3，4}（CUA）B=（1，3，4，5），又
B={3，4} 
CUA={1，4，5} 故A只有等于集合{2，3}
P=-（3+4）=-7 q=2×3=6
7．方程x2-ax-b=0的解集为{2，3}，由韦达定理a=2+3=5,b=2×3=6,不等式bx2-ax+1>0化为6x2-5x+1>0
解得{x
}
8.由AB
知方程组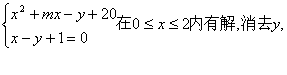
得x2+(m-1)x=0
在0x
内有解，
即m3或m-1。
若3，则x1+x2=1-m<0,x1x2=1,所以方程只有负根。
若m-1,x1+x2=1-m>0,x1x2=1,所以方程有两正根，且两根均为1或两根一个大于1，一个小于1，即至少有一根在[0，2]内。
因此{m
<m-1}。