![]() 高一(上)数学检测试卷
高一(上)数学检测试卷
一. 选择题(每小题4分,共60分)
1 设集合![]() 用A表示,则下列各式中正确的是( )
用A表示,则下列各式中正确的是( )
A 0![]() B
B ![]()
![]() C
C ![]() D
D ![]()
2 若点P的坐标![]() ,则P点所在象限为( )
,则P点所在象限为( )
A第一或第二象限B第二或第三象限C第三或第四象限D第一或第四象限
3 集合M=![]() , N=
, N=![]() ,则M与N的关系是( )
,则M与N的关系是( )
A M![]() N
B M
N
B M![]() N
C M=N D M
N
C M=N D M![]() N
N
4 集合M=![]() , N=
, N=![]() , M
, M![]() N=
N=![]() ,则
,则![]() 的值为( )
的值为( )
A -2 B - 1 C 1 D 2
5 ![]() ,则
,则![]() (
(![]() )= ( )
)= ( )
A 1 B 3 C 15 D 30
6 计算![]() 的结果是(
)
的结果是(
)
A ![]() B
B ![]() C
C ![]() D
D ![]()
![]()
7 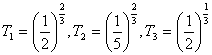 , 则( )
, 则( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
8 在下列区间中,使函数![]() 不存在反函数的区间是( )
不存在反函数的区间是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
9 函数![]() 的反函数的定义域是( )
的反函数的定义域是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
10 计算![]() =( )
=( )
A 14 B 220 C 8 D 22
11 在数列 1 , ![]() , 3 ,
, 3 ,![]() ,
,![]() ,… 中,
,… 中,![]() 是该数列的( )
是该数列的( )
A 第11项 B 第12项 C 第13项 D 第10项
12已知![]() 是等差数列,
是等差数列,![]() ,则该数列的通项公式是( )
,则该数列的通项公式是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
13 若![]() ﹑b﹑c成等比数列,则
﹑b﹑c成等比数列,则![]() 的图象与
的图象与![]() 轴的交点个数为( )
轴的交点个数为( )
A 0 B 1 C 2 D 不能确定
14 一个项数是偶数的等比数列,它的偶数项的和是奇偶数项的和的2倍,又它的首项为1,且中间两项之和为24.则此等比数列的项数是( )
A 12 B 14 C 20 D 122
15 已知一个等比数列和一个首项为0的等差数列的对应项相家得到一个数列![]() ,其中,
,其中,![]() ,则
,则![]() 等于( )
等于( )
A 466 B 467 C 978 D 1068
二 填空题( 每小题4分,共40分)
16 已知![]() 的图象过点(0,1),则
的图象过点(0,1),则![]() 的反函数的图象过点 .
的反函数的图象过点 .
17 函数![]() 的图象恒过定点
.
的图象恒过定点
.
18 函数![]() 的定义域是
的定义域是![]() ,则
,则![]() 的取值范围是
.
的取值范围是
.
19 若函数![]() 上是减函数, 则
上是减函数, 则![]() 的取值范围是
.
的取值范围是
.
20 ![]() .
.
21方程![]() 的解的个数是
.
的解的个数是
.
22如果方程![]() 有两个相异实数根, 则
有两个相异实数根, 则![]() 的取值范围是
.
的取值范围是
.
23 已知正数等差数列![]() ,则它的前12项之和为 .
,则它的前12项之和为 .
24 三个不同的实数![]() ﹑b﹑c成等差数列,且
﹑b﹑c成等差数列,且![]() ﹑c﹑b成等比数列,则
﹑c﹑b成等比数列,则![]() :b:c= .
:b:c= .
25 在等比数列![]() .
.
三 解答求证题(每小题10分,共50分)
26设等差数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() 。
。
(I)求数列![]() 的通项公式及前n项和公式;
的通项公式及前n项和公式;
(II)求和![]() 。
。
27有一批国产彩电,原销售价为每台2000元,甲、乙两家商场均有销售,甲商场用如下方法促销,购买一台优惠2.5%,购买两台优惠5%,购买三台优惠7.5%,依次类推,但每台最低价不能低于1500元,乙商场一律按原销售价的80%销售,某单位需购买一批此类彩电,问去哪家商场购买费用较少?请说明理由。
28设数列![]() 中各项都是正数,前
中各项都是正数,前![]() 项之和为
项之和为![]() ,且
,且![]() 与3的等差中项恰是
与3的等差中项恰是![]() 与3的等比中项。
与3的等比中项。
(I)求数列![]() 的通项公式;
的通项公式;
(II)若数列![]() 中,
中,![]() ,求数列
,求数列![]() 的前n项之和
的前n项之和![]() 的表达式;
的表达式;
29设二次函数![]() ,方程
,方程![]() 的两个实数根为
的两个实数根为![]()
(I)若![]() ,求证:函数
,求证:函数![]() 在区间
在区间![]() 上是单调减函数;
上是单调减函数;
(II)若![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
30李师傅经营报刊亭多年,闲暇之余,他经常对一些热销期刊的销售情况进行统计分析,从而对来年的预订量进行调整。例如,畅销季刊《×××》规定,杂志的零售价为5元/本,卖报人可以以3.5元/本的价格预订一年4期杂志,每期的数量必须相同,中途不得更改订量。如果杂志卖了有剩余,杂志社将在年底以1.5元/本的价格回收,来年以合订本的形式再发售。因此,如果预订量不当,李师傅发售这本杂志会出现赔或脱销的情况,这对他的经营收入都会产生影响。下表是李师傅对自己在2003年发售这本杂志的情况进行的一个统计。
李师傅2003年出售杂志《×》的情况统计表:
| 期 号 | 1 | 2 | 3 | 4 |
| 预订份数 | 150 | 150 | 150 | 150 |
| 脱销份数 | 9 | 2 | 7 | |
| 剩余份数 | 4 |
2004年的征订工作即将就要开始,请你为李师傅计算一下,他每期应预订多少本,才能使其经销此杂志的年收益最大?
高一(上)数学检测试卷参考答案
一 选择题(每小题4分,共60分)
1B 2C 3 A 4B 5C 6C 7D 8 B
9 D 10D 11B 12B 13A 14C 15 C
二 填空题( 每小题4分,共40分)
16 (4,1) 17 (3,-2) 18 (0,1) 19 ![]() 20
20 ![]()
21 3 22 ![]() 23 48 24 4:1:(-2) 25
23 48 24 4:1:(-2) 25 ![]()
三 解答求证题(每小题10分,共50分)
26(本小题满分10分)
解(I)由![]()
得![]()
![]()
(II)解![]() 且
且![]() ,得
,得![]()
因此,原式![]()
27(本小题满分10分)
解:设该单位要购买x台彩电,则在甲商场购买的费用为
![]()
在乙商场购买x台彩电的费用为
![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
若![]() ,则
,则![]()
若![]() ,则
,则![]()
若![]() ,则
,则![]()
综上,若购买不超过7台,到乙商场;若购买8台到甲或乙商场;若购买超过8台到甲商场购买。
28. (本小题满分10分)
解:(I)依题意,有
![]() ,
,
即![]() ,
,
![]()
两式作差,得 ![]() ,
,
即![]() ,
,
![]()
![]() 数列
数列![]() 中各项都是正数,即
中各项都是正数,即![]() ,
,
![]() ,
,
即数列![]() 成等差数列,公差为6。
成等差数列,公差为6。
又![]() ,
,
![]() ,
,
即
(II)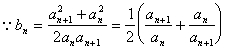
![]()
![]()
29. (本小题满分10分)
解法一:方程![]() ,即
,即![]()
设![]()
(I)由题知,![]() 的两个根
的两个根![]() 满足
满足![]() ,
,
当且仅当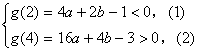
由(1)得,![]()
![]() (3)
(3)
由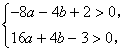 得
得![]() ,即
,即![]()
结合(3),得![]() .
.
![]() 函数
函数![]() 在区间
在区间![]() 上是单调减函数,
上是单调减函数,
![]() 函数
函数![]() 在区间
在区间![]() 上是单调减函数;
上是单调减函数;
(II)![]() 同号
同号
由![]() ,得
,得![]()
又![]() ,
,
![]() 若
若![]() ,则
,则![]()
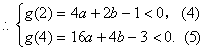
![]()
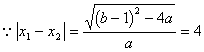 ,
,
![]()
根据(4),(5)得
得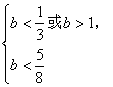
结合![]() ,得
,得![]() ;
;
(2)若![]() ,则
,则![]()
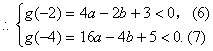
![]()
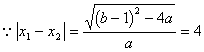 ,
,
![]()
根据(6),(7)得
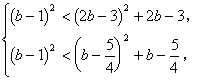
得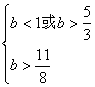
结合![]() 得
得![]()
综上,实数b的取值范围是![]()
解法二:方程![]() ,即
,即![]()
设![]()
(I)由题知,![]() 的两个根
的两个根![]() 满足
满足![]() ,
,
当且仅当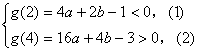
![]() ,得
,得![]()
![]() 函数
函数![]() 在区间
在区间![]() 上是单调减函数,
上是单调减函数,
![]() 函数
函数![]() 在区间
在区间![]() 上是单调减函数;
上是单调减函数;
(II)![]() 方程
方程![]() 的两个根
的两个根![]() ,
,
![]() 同号,
同号,
又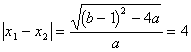 ,
,
![]()
![]() (1)若
(1)若![]() ,则
,则
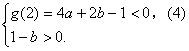
![]() ,
,
从而![]()
解得 ![]() 或
或![]()
结合![]() ,得
,得![]()
![]() ,得
,得![]()
(2)若![]() ,则
,则
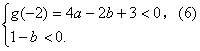
![]() ,
,
从而![]()
仍得 ![]() ,从而得
,从而得![]()
综上,实数![]() 的取值范围是
的取值范围是![]()
30. (本小题满分10分)
解:设每期预订![]() 本,年收益为
本,年收益为![]() 。由题知,发售1本杂志赚1.5元,而剩余1本杂志赔2元,因此对于1本杂志而言,售出与剩余之间就相差3.5元。从统计表中可以看出,在预订150本/月的前提下,4期杂志,有3期脱销,1期过剩,期销量最小是146本。如果每期预订量不超过146本,则全部售完 ;当每期预订量超过146本时,有的期刊就要有剩余。因此,如果每期预订量为
。由题知,发售1本杂志赚1.5元,而剩余1本杂志赔2元,因此对于1本杂志而言,售出与剩余之间就相差3.5元。从统计表中可以看出,在预订150本/月的前提下,4期杂志,有3期脱销,1期过剩,期销量最小是146本。如果每期预订量不超过146本,则全部售完 ;当每期预订量超过146本时,有的期刊就要有剩余。因此,如果每期预订量为![]() ,则每期的剩余量可见下表:
,则每期的剩余量可见下表:
| 预订量 | 各期剩余量 | 剩余总量 | |||
| 1 | 2 | 3 | 4 | ||
|
| 0 | 0 | 0 | 0 | 0 |
|
| 0 | 0 |
| 0 |
|
|
| 0 |
|
| 0 |
|
|
| 0 |
|
|
|
|
|
|
|
|
|
|
|
因此,预订量与年收益的函数关系是:
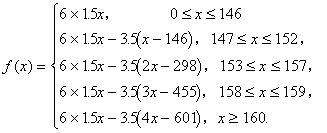
比较各段表达式中![]() 的系数,可知
的系数,可知![]() 时,
时,![]() 是增函数;
是增函数;![]() 时,
时,![]() 是减函数。
是减函数。
![]() ,
,
![]() ,
,
![]()
答:李师傅每个月应预订157本《×××》杂志,才能使其经销此杂志的年收益最大。
备注:这是一份练习试题,估计有些难度,尤其大题难度有点大.