第十七教时
教材：正弦定理
目的：要求学生掌握正弦定理，并能应用解斜三角形，解决实际问题。
过程：一、引言：在直角三角形中，由三角形内角和定理、勾股定理、锐角三角函数，可以由已知的边和角求出未知的边和角。
那么斜三角形怎么办？——提出课题：正弦定理、余弦定理
二、1．特殊情况：直角三角形中的正弦定理：
sinA=
sinB=
sinC=1 即：
c=
c=
c=
∴==
2．能否推广到斜三角形？
证明一（传统证法）在任意斜△ABC当中：
S△ABC=
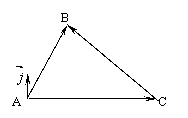两边同除以
即得：==
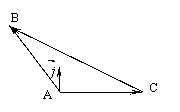3．用向量证明：
证二：过A作单位向量
垂直于
+
=
两边同乘以单位向量
•(+)=•
则：•+•=•
∴•cos90°+•cos(90°-C)=•cos(90°-A)
∴
∴=
同理：若过C作垂直于得： = ∴==
当△ABC为钝角三角形时，设 ÐA>90° 过A作单位向量垂直于向量
4．突出几点：1°正弦定理的叙述：在一个三角形中。各边和它所对角的正弦
比相等，即：==它适合于任何三角形。
2°可以证明===2R （R为△ABC外接圆半径）
3° 每个等式可视为一个方程：知三求一
三、正弦定理的应用
从理论上正弦定理可解决两类问题：
1．两角和任意一边，求其它两边和一角；
2．两边和其中一边对角，求另一边的对角，进而可求其它的边和角。
例一、在△ABC中，已知
A=45° C=30° 求b（保留两个有效数字）
解略 见P128 注意强调“对”
例二、在△ABC中，已知
b=28 A=40°
求B (精确到1°)和c（保留
两个有效数字）
解略 见P129 注意由=求出sinB=0.8999 B角有两解
例三、在△ABC中，已知
b=50 A=38°
求B (精确到1°)和c（保留
两个有效数字）
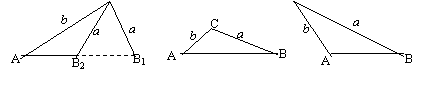
解略 见P129 注意由b<a, 得B<A ∴B必为锐角只有一解与例二比较
四、小结：正弦定理，两种应用
|
|
|
 | |||
 | |||
一解 两解 一解
五、作业：P131练习1、2 P132 1、2、3