第十九教时
教材：正弦定理和余弦定理的复习《教学与测试》76、77课
目的：通过复习、小结要求学生对两个定理的掌握更加牢固，应用更自如。
过程：一、复习正弦定理、余弦定理及解斜三角形
二、例一 证明在△ABC中
=
=
=2R，其中R是三角形外接圆半径
证略 见P159
注意：1．这是正弦定理的又一种证法(现在共用三种方法证明)
2.正弦定理的三种表示方法(P159)
例二 在任一△ABC中求证：
证：左边=
=
=0=右边
例三 在△ABC中，已知
，
，B=45° 求A、C及c
解一：由正弦定理得：
∵B=45°<90° 即b<a ∴A=60°或120°
当A=60°时C=75° 
当A=120°时C=15° 
解二：设c=x由余弦定理 
将已知条件代入，整理：
解之：
当
时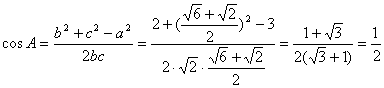
从而A=60° C=75°
当
时同理可求得：A=120°
C=15°
例四 试用坐标法证明余弦定理
证略见P161
例五 在△ABC中，BC=a, AC=b, a, b是方程
的两个根，且
2cos(A+B)=1 求 1°角C的度数 2°AB的长度 3°△ABC的面积
解：1°cosC=cos[p-(A+B)]=-cos(A+B)=-
∴C=120°
2°由题设：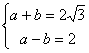
∴AB2=AC2+BC2-2AC•BC•osC
即AB=
3°S△ABC=
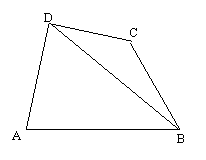例六 如图，在四边形ABCD中，已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长
解：在△ABD中，设BD=x
则
即
整理得：
解之：
（舍去）
由余弦定理：
∴
例七 （备用）△ABC中，若已知三边为连续正整数，最大角为钝角，
1°求最大角 2°求以此最大角为内角，夹此角两边之和为4的平行四边形的最大面积。
解：1°设三边
且
∵C为钝角 ∴
解得
∵
∴
或3 但时不能构成三角形应舍去
当
时 
2°设夹C角的两边为
S
当
时S最大=
三、作业：《教学与测试》76、77课中练习
补充：1．在△ABC中，求证：
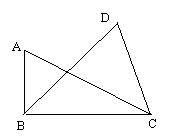
2．如图AB^BC CD=33 ÐACB=30°
ÐBCD=75°
ÐBDC=45° 求AB的长 