指数 指数函数
【重点难点解析】
1．本单元的知识结构
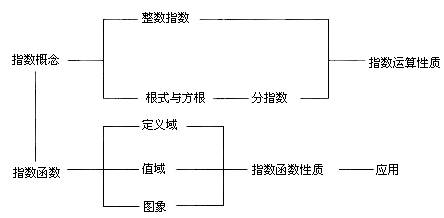
2．指数概念由特殊乘法运算定义，是乘法运算的发展，是人类探索化简运算的过程中，创造并发展的数学知识；它由正整数指数开始，到负整数指数、零指数，再到分式指数(根式)，最后到实数指数．
3．指数运算的特点是强概念性及性质使用而弱计算性，所以指数的运算性质及方根表示既是重点也是难点．
4．指数函数的概念及性质是重点，指数函数的值域易被忽视而成为难点．
【考点】
1．指数运算一般结合其他知识在应用中进行考查．
2．根式及方根运算与指数函数的图象和性质，几乎每年高考都要涉及．
【典型热点考题】
例1 完成下列计算：
(1)
； (2)
；
(3)
； (4)
；
(5)
； (6)
．
思路分析
运算时，一般将根式化为分指数，运用指数运算性质进行化简计算，但要注意的是分指数的运算实质是方根的化简，必须依照方根运算的要求进行，即注意根指数(分指数的分母)的奇偶性来决定结果，一般偶次方根化简时尤须注意．
解：
(1)
＝－3．
(2)
＝2．
(3)
．
(4)
．
(5)
．
(6)
＝27000．
例2 化简下列各式：
(1)
；
(2)
．
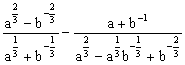思路分析
多项式的乘法公式，本质上给出的是多项式的次数与它的因式的次数间的关系(当然也有多项式中的运算及形式的关系)，引入分指数的概念后，这种公式的本质并未改变，只不过由于指数形式的复杂，使它们指数间的倍比关系较难判断清楚，因此就给如何应用公式分解因式并化简带来了困难，只要抓住多项式及根式化简的通法、通性，这些难题不会造成困难．
解：
(1)
当a>b≥0时，
∴
当b≥a≥0时，
∴
＝0．
(2)解法一：
．
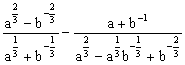
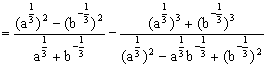
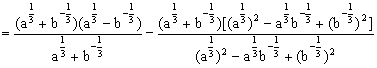
解法二：
设
，
∴
∴
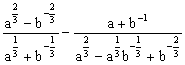
＝m－n－(m＋n)
＝－2n
．
点评 不要认为设辅助未知数只是一种可有可无的运算技巧，其实设辅助未知数是对数学问题的“层次性”的深刻认识的表现，是把复杂问题转化为两个或多个基本问题的重要的分析思维的具体表达．
例3 化简下列各式：
(1)
；
(2)
；
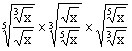(3)
．
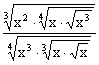思路分析
用根式计算时，必须将根式化为同次根式才能进行乘、除、幂的计算，若式子中有重根式(根号套根号)的形式，化同次根式更难更容易出错；如果逐层将根号处理为分指数，再用指数的运算性质运算既简捷又方便．
解：
(1)
．
(2)
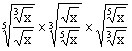
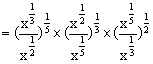
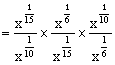
＝1．
(3)
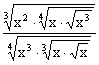
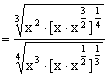
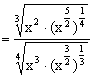
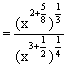
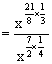
＝1．
点评 重根式化简只需作1～3个题，通过具体演算达到了解方法的目的即可．
例4 求下列函数的定义域和值域：
(1)
；
(2)
．
思路分析
因为一般指数函数
(a>0且a≠1)的定义域是一切实数，值域是(0，＋∞)，所以复杂的与指数函数有关的定义域、值域问题，主要考虑与自变量有关的代数式的运算限制和取值范围，就可以解出定义域；但值域问题一方面考虑指数函数的单调性，同时必须兼顾“指数函数”的值域是(0，＋∞)．
解：
(1)
∴函数的定义域是[2，＋∞)
∵x∈[2，＋∞)时，x－2≥0
∴
∵3>1，以3为底数的指数函数是增函数
∴
∴函数的值域是[1，＋∞)．
(2)∵
中x≠0
∴函数的定义域是{xx≠0且x∈R}
∵x≠0时，
∴
，而
∴函数的值域是{yy>0且y≠1}．
例5 求下列关于x的不等式的解集．
(1)
；
(2)a>0且a≠1时，
．
思路分析
因为不等式中的变量x在指数部分，所以这类不等式(称指数不等式)的解法是：利用指数函数的单调性，将各不等式先转化为一般的一元一次不等式，一元二次不等式及不等式组求解，由此看来，函数的单调性是用来处理与函数有关的量大小比较的有力工具．
解：
∵6>1，则以6为底的指数函数是增函数
∵
∴
∴－2<x<1
∴不等式的解集为{x－2<x<1}．
(2)∵
当a>1时，以a为底的指数函数是增函数
∴
⊿＝
∴不等式的解集为R．
当0<a<1时，以a为底的指数函数是减函数
∴
⊿＝
∴
∴a>1时不等式的解集是R，
0<a<1时，不等式的解集是
．
例6 设
(a为实数)
(1)x∈R，试讨论f(x)的单调性，并且用单调性定义给出证明；
(2)当a＝0时，若函数y＝g(x)的图象与y＝f(x)的图象关于直线x＝1对称．求函数y＝g(x)的解析式．
解：
(1)(i)a＝0时，
任取
，
∵
∵
，
∴
∴
∴函数f(x)是增函数．
(ii)a<0时，f(x)是增函数，下面给出证明：
任取，
∵
∵，
∴
又∵a<0，
∴
∴
从而得：函数f(x)是增函数．
(iii)令
，
0<a<1时
f(x)＝1时，
可得：
又∵是增函数
∴存在
，有：
，
也就是：存在两个实数
，，但有
∴0<a<1时，f(x)在全体实数R上不是单调函数
a＝1时，∵f(x)＝3时，可得：
又∵是增函数
∴存在，有：
，
也就是：存在两个实数，，但有
∴a＝1时，f(x)在全体实数R上不是单调函数
a>1时，f(x)也不是单调函数．(请读者自己给出证明)
(2)在函数y＝g(x)的图象上取一点P(x，y)，点P关于直线x＝1的对称点
从而，得：
∵函数y＝g(x)的图象与函数y＝f(x)的图象关于直线x＝1对称
∴在y＝f(x)的图象上
也就是：
从而，可得：
也就是：
．
点评 函数f(x)不是单调函数
存在，，但有
．
【同步达纲练习】
一、选择题
1．若
，则a＋b的值是( )
A．－18 B．18
C．－2 D．2
2．函数
的定义域是( )
A．(－1，2] B．(－∞，2]
C．(－∞，－1)∪(－1，2] D．(－∞，－1)
3．代数式
的值是( )
A．
B．
C．
D．
4．已知
，则m、n的关系是( )
A．1>m>n>0 B．1>n>m>0
C．m>n D．m<n
5．代数式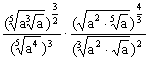
的值是( )
A．1 B．
C．
D．以上答案均不正确
6．函数
(其中a>1)( )
A．在(－∞，0)上是增函数 B．在[0，＋∞)上是增函数
C．增函数 D．减函数
7．若
，则实数a、b间应该有的关系是( )
A．a>b B．a＝b
C．a<b D．以上答案都可能成立
8．三个数
，则a、b、c的关系是( )
A．a<b<c B．a<c<b
C．b<a<c D．b<c<a
9．若指数函数
在(－∞，＋∞)上是减函数，那么( )
A．0<a<1 B．－1<a<0
C．a＝－1 D．a<－1
二、填空题
1．函数
的定义域是____________________．
2．当x＝4时，代数式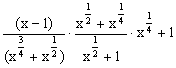
的值是____________________．
3．化简代数式：
＝____________________．(其中m、n都是自然数且m≠n)
4．若
，则x＝____________________．
5．
＝____________________．
三、解答题
用定义证明：函数
在区间(－∞，0]上是减函数．
四、选择题
1．若
，则a＋b的值是( )
A．1 B．5
C．－1 D．2π－5
2．函数
的定义域是( )
A．[4，＋∞) B．(－∞，2)
C．(2，4] D．(－∞，2)∪[4，＋∞)
3．代数式
的值是( )
A．
B．
C． D．
4．若
且m>n>1，则实数a的取值范围是( )
A．(1，＋∞) B．(1，π)
C．(0，π－1) D．(－∞，π－1)
5．已知
，则这样的x值( )
A．存在且有且只有一个 B．存在且不只一个
C．存在且x<2 D．根本不存在
6．函数
(其中a>0且a≠1)，若对m<n<0有f(m)>f(n)成立，则a的取值范围是( )
A．(0，1) B．(1，＋∞)
C．(－1，0)∪(0，1) D．(－∞，－1)∪(1，＋∞)
7．若
，则x的值是( )
A．1 B．－1
C．4 D．6
8．已知
，则a、b、c的大小关系是( )
A．a>b>c B．b>a>c
C．c>a>b D．b>c>a
9．函数
在区间(－∞，0)上的单调性是( )
A．增函数 B．减函数
C．常数 D．有时是增函数有时是减函数
五、填空题
1．已知
，使
的x的值的集合是____________________．
2．函数
的定义域是集合____________________．
3．满足
的x的值的集合是____________________．
4．函数
的定义域是[－1，2]，则函数f(x)的定义域是____________________．
5．指数函数
的图象经过点(2，
)，则底数a的值是____________________．
六、解答题
1．当
，
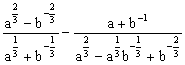时，求代数式的值．
2．求使不等式
成立的x值的集合．(其中a>0且a≠1)
参考答案
【同步达纲练习】
一、
1．D
2．C
提示：
要求x≠－1即可．
3．A 4．D 5．D
6．D
提示：
7．D
提示：a>b>0时，可能成立，当a<b<0时，可能成立，当a＝b＝0时，
8．C
9．B
提示：底数满足0<a＋1<1．
二、
1．(－∞，5]
2．2
提示：
3．
4．
提示：
5．9
三、
证明：设
是区间(－∞，0]上的任意两个值，
∴
∵
函数
是增函数
∴
，
，
∴
∴
即
∴f(x)在区间(－∞，0]上是减函数．
四、
1．A
提示：
，
．
2．D
3．A
提示：
．
4．D
提示：
．
5．A
提示：作函数
图象，看y＝10时的图象上的点的x值．
6．B
提示：f(x)是偶函数作出图象观察．
7．D
提示：
8．B
提示：c<0，
，0<a<3．
9．B
提示：
五、
1．{xx>0}
2．{xx≥0}
提示：
．
3．
提示：
，
无解．
4．
提示：－1≤x≤2，则
．
5．
提示：
且a>0
六、
1．解：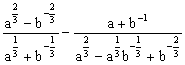
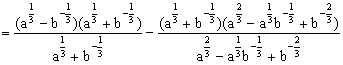
当时，
∴
∴
．
2．解：∵
∴原不等式化为：
当a>1时，函数是增函数
∴
∴－2<x<4
当0<a<1时，是减函数
∴
∴x<－2或x>4
∴当a>1时，x值集合是{x－2<x<4}；当0<a<1时，x值的集合是{xx<－2或x>4}．