同步测控优化训练B卷(指数函数与对数函数)
说明:本试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填入题后括号内,第Ⅱ卷可在各题后直接作答.共100分,考试时间90分钟.
第Ⅰ卷(选择题 共30分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.设f:x→y=2x是A→B的映射,已知集合B={0,1,2,3,4},则A满足( )
A.A={1,2,4,8,16} B.A={0,1,2,log23}
C.A![]() {0,1,2,log23} D.不存在满足条件集合
{0,1,2,log23} D.不存在满足条件集合
考查映射概念、指数、对数运算.
【解析】 A中每个元素在集合中都有象,令2x=0,方程无解.
分别令2x=1,2,3,4,解得x=0,1,log23,2.
【答案】 C
2.设P={yy=x2,x∈R},Q={yy=2x,x∈R},则( )
A.Q=P B.Q![]() P C.P∩Q={2,4} D.P∩Q={(2,4)}
P C.P∩Q={2,4} D.P∩Q={(2,4)}
考查集合间关系及函数值域.
【解析】 P=[0,+∞),Q=(0,+∞).
【答案】 B
3.已知函数f(x)=loga(2-ax)在[0,1]上为减函数,则a的取值范围是( )
A.(0,1) B.(1,2) C.(0,2) D.[2,+∞)
考查对数函数定义域及单调性.
【解析】 由y=loga(2-ax)单调性及2-ax>0对任意x∈[0,1]恒成立,可求得1<a<2.
【答案】 B
4.已知函数f(x)=![]() 时f[f(
时f[f(![]() )]的值是( )
)]的值是( )
A.9 B.![]() C.-9 D.-
C.-9 D.-![]()
考查对分段函数对应法则的理解.
【解析】 f(![]() )=log2
)=log2![]() =-2,
=-2,
f(-2)=3-2=![]()
【答案】 B
5.若函数f(x)=log2(x-1)+log2(x+2)的反函数为g(x),则g(2)等于( )
A.1 B.-3 C.2 D.2或-3
考查对数函数及互为反函数间的函数关系.
【解析】 依题意![]()
![]() x=2
x=2
【答案】 C
6.已知f(x)=ax,g(x)=logax(a>0且a≠1),若f(3)g(3)<0,则f(x)与g(x)在同一坐标系内的图象可能是( )
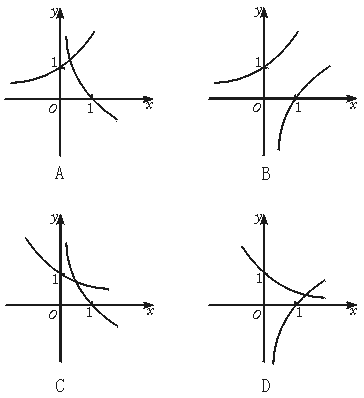
【解析】 ∵f(3)=a3>0,∴g(3)=loga3<0,∴0<a<1
【答案】 C
7.若函数y=log![]() (2-log2x)的值域是(-∞,0),则其定义域是( )
(2-log2x)的值域是(-∞,0),则其定义域是( )
A.x<2 B.0<x<2 C.0<x<4 D.2<x<4
考查对数函数定义域、值域.
【解】 令2-log2x=u,由题意知u>1,![]() log2x<1,故0<x<2.
log2x<1,故0<x<2.
【答案】 B
8.若定义运算a*b=![]() ,则函数f(x)=3x*3-x的值域是( )
,则函数f(x)=3x*3-x的值域是( )
A.(0,![]() B.[1,+
B.[1,+![]() C.(0,+∞) D.(-∞,+∞)
C.(0,+∞) D.(-∞,+∞)
考查函数值域及灵活运用能力.
【解析】 若3x≥3-x,即x≥0,则f(x)=3-x
若3x<3-x,即x<0,则f(x)=3x
故值域为(0,1]
【答案】 A
9.若x0是方程2x=![]() 的解,则x0∈( )
的解,则x0∈( )
A.(0.1,0.2) B.(0.3,0.4) C.(0.5,0.7) D.(0.9,1)
考查指数函数图象性质及估算能力.
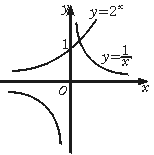 【解析】 画出y=2x,y=
【解析】 画出y=2x,y=![]() 图象.
图象.
∵20.1<20.2<1,而![]() >
>![]() =5
=5
排除A,同理排除B
20.5=![]() ≈1.414,20.7>20.5,
≈1.414,20.7>20.5,
而![]() =2,
=2,![]() ≈1.428
≈1.428
21>20.9>20.5≈1.414,而![]() ≈1.11
≈1.11
【答案】 C
10.今有一组实验数据如下:
| t | 1.99 | 3.0 | 4.0 | 5.1 | 6.12 |
| v | 1.5 | 4.04 | 7.5 | 12 | 18.01 |
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( )
A.v=log2t B.v=log![]() t C.v=
t C.v=![]() D.v=2t-2
D.v=2t-2
考查构建数学模型的能力,具开放性.
【解析】 五组数据,取近似值1.99≈2;4.04≈4;5.1≈5,18.01≈18,
代入验证可知v=![]() 最接近.
最接近.
【答案】 C
第Ⅱ卷(非选择题 共70分)
二、填空题(本大题共4小题,每小题4分,共16分)
11.方程log3(1-2·3x)=2x+1的解x=______.
考查对数与指数运算.
【解析】 32x+1=1-2·3x,即3(3x)2+2·3x-1=0
解得3x=![]() ,故x=-1
,故x=-1
【答案】 -1
12.函数f(x)=ax(a>0且a≠1)在区间[1,2]上的最大值比最小值大![]() ,则a的值为______.
,则a的值为______.
考查指数函数的单调性及解决问题的能力.
【解析】 当a>1时,f(x)为增函数,a2-a=![]() ,得a=
,得a=![]()
当0<a<1时,f(x)=ax在[1,2]上为减函数,
有a-a2=![]()
![]() a=
a=![]() ,
,
故a=![]() 或
或![]()
【答案】 ![]() 或
或![]()
13.设函数f(x)=![]() ,则满足f(x)=
,则满足f(x)=![]() 的值为______.
的值为______.
考查分段函数对应法则理解及对数运算.
【解析】 若x∈(-∞,1),有2-x=![]() ,∴x=2,但2
,∴x=2,但2![]() (-∞,
(-∞,![]() ;
;
若x∈(1,+∞),有log81x=![]()
∴x=3符合题意
【答案】 3
14.国家规定的个人稿酬纳税方法是:不超过800元的不纳税,超过800元而不超过4000元的按超过800元的14%纳税;超过4000元按全部稿酬的11%纳税,某人出版了一本书,共纳税420元,他的稿费为______元.
考查函数应用及解决实际问题的能力.
【解析】 若其稿费为4000,则应纳税3200×14%=448>420
故稿费应小于4000元,设为x元
则(x-800)14%=420,解得x=3800(元)
【答案】 3800
三、解答题(本大题共5小题,共54分,解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分8分)已知函数f(x)=![]() +lg
+lg![]() .
.
(1)求此函数的定义域,并判断函数单调性.
(2)解关于x的不等式f[x(x-![]() )]<
)]<![]() .
.
【解】 (1)f(x)=![]() +lg
+lg![]() =
=![]() +lg(-1+
+lg(-1+![]() )
)
要使f(x)有意义,即![]() >0,∴f(x)的定义域为-1<x<1
>0,∴f(x)的定义域为-1<x<1
设-1<x1<x2<1,则f(x1)-f(x2)=lg(-1+![]() )-lg(-1+
)-lg(-1+![]() )
)
∵-1<x1<x2<1,∴0<x1+1<x2+1
∴-1+![]() >-1+
>-1+![]()
∴f(x1)>f(x2),即f(x)在(-1,1)上为减函数
(2)∵f(0)=![]() ,∴f[x(x-
,∴f[x(x-![]() )]<
)]<![]() =f(0)
=f(0)
由(1)知f(x)在(-1,1)上为奇函数
∴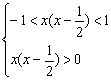 ,解得:
,解得:![]()
即不等式解集为(![]() ,0)∪(
,0)∪(![]() ,
,![]() )
)
16.(本小题满分10分)已知y=log4(2x+3-x2).
(1)求定义域;
(2)求f(x)的单调区间;
(3)求y的最大值,并求取最大值时x值.
考查对数函数、二次函数的单调性、最值.
【解】 (1)由2x+3-x2>0,解得-1<x<3
∴f(x)定义域为{x-1<x<3}
(2)令u=2x+3-x2,则u>0,y=log4u
由于u=2x+3-x2=-(x-1)2+4
再考虑定义域可知,其增区间是(-1,1),减区间是[1,![]()
又y=log4u为(0,+∞)增函数,
故该函数单调递增区间为(-1,1],减区间为[1,3)
(3)∵u=2x+3-x2=-(x-1)2+4≤4
∴y=log4u≤log44=1
故当x=1时,u取最大值4时,y取最大值1.
17.(本小题满分12分)已知函数f(x)=2x-x2(x≥0),问是否存在这样的正数a、b,当x∈[a,b]时g(x)=f(x),且g(x)值域[![]() ,
,![]() ]?若存在,求出所有a、b之值,若不存在,请说明理由.
]?若存在,求出所有a、b之值,若不存在,请说明理由.
考查函数知识综合运用,分类讨论思想.
【解】 分三种情况讨论:
①当0<a<b≤1时,那么![]() >1,而当x≥0时,f(x)的最大值为1,故此时不可能使g(x)=f(x)
>1,而当x≥0时,f(x)的最大值为1,故此时不可能使g(x)=f(x)
②当0<a<1<b时,则g(x)最大值为g(1)=f(1)=1,
即![]() =1,得a=1与0<a<1<b矛盾
=1,得a=1与0<a<1<b矛盾
③当1≤a<b时,∵x≥1,f(x)为减函数,
则g(x)=f(x)=2x-x2,于是有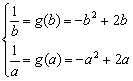
即![]()
∵1≤a<b,∴a=1,b=![]()
18.(本小题满分12分)若p∈R,且当log2p<2时,不等式px+1>2x-p恒成立,试求x的取值范围.
考查对数基本概念及分类讨论思想.
【解】 由log2p<2得-2<log2p<2,则![]() <p<4
<p<4
由不等式px+1>2x-p,得p(x+1)>2x-1
①当x>-1时,![]() <p,即
<p,即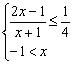 ,解得-1<x≤
,解得-1<x≤![]()
②当x<-1时,![]() >p,即
>p,即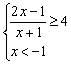 ,解得-
,解得-![]() ≤x<-1
≤x<-1
∴x的取值范围为(-1,![]() ∪[-
∪[-![]() ,-
,-![]()
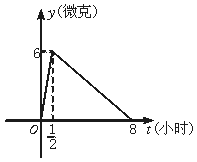 19.(本小题满分12分)某医药研究所开发一种新药,如果成人按规定的剂量使用,据监测,服药后每毫升血液中的含药量y与时间t之间近似满足如图曲线
19.(本小题满分12分)某医药研究所开发一种新药,如果成人按规定的剂量使用,据监测,服药后每毫升血液中的含药量y与时间t之间近似满足如图曲线
(1)写出服药后y与t之间的函数关系式;
(2)据测定,每毫升血液中含药量不少于4微克时治疗疾病有效,假若某病人一天中第一次服药为7:00,问一天中怎样安排服药时间、次数,效果最佳?
考查函数应用及分析解决问题的能力.
【解】 (1)依题意,得y=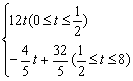
(2)设第二次服药时,在第一次服药后t1小时
则-![]() t1+
t1+![]() =4,t1=3
=4,t1=3
因而第二次服药应在10:00
设第三次服药在第一次服药后t2小时,则此时血液中含药量应为两次服药后含药量之和,即有-![]() t2+
t2+![]() -
-![]() (t2-3)+
(t2-3)+![]() =4
=4
解得:t2=7(小时)
设第四次服药在第一次服药后t3小时(t3>8),则此时第一次服的药已吸收完,此时血液中含药量应为第二、三次之和
-![]() (t3-3)+
(t3-3)+![]() +[-
+[-![]() (t3-7)+
(t3-7)+![]() ]=4
]=4
解得t3=10.5小时
故第四次服药应在17:30.