指数函数与对数函数同步训练A卷

指数函数与对数函数同步训练A卷

 

说明：本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案填入题后括号内，第Ⅱ卷可在各题后直接作答.共100分，考试时间90分钟.

第Ⅰ卷(选择题　共30分)

一、选择题(本大题共10小题，每小题3分，共30分)

1.已知2lg(x－2y)=lgx+lgy,则的值为（　　）

A.1　　　　　　　　　　　　　　　B.4　　　　　　　　　　　　　　　C.1或4　　　　　　　　　　　 D.或4

考查对数函数及对数函数定义域.

【解析】 原命题等价x=4y

∴=4

【答案】 B

2.函数y=log(x²－6x+17)的值域是（　　）

A.R　　　　　　　　　　　　　　 B.［8，+　　　　　　　　C.(－∞,－　　　　　　　 D.［－3,+∞)

考查对数函数单调性、定义域、值域.

【解析】 y=log［(x－3)²+8］≤log8=－3

【答案】 C

3.若a>1,b>1,且lg(a+b)=lga+lgb,则lg(a－1)+lg(b－1)的值等于（　　）

A.0　　　　　　　　　　　　　　　B.lg2　　　　　　　　　　　　　　C.1　　　　　　　　　　　　　　　D.－1

考查对数运算.

【解析】 由lg(a+b)=lga+lgba+b=ab

即(a－1)(b－1)=1,∴lg(a－1)+lg(b－1)=0

【答案】 A

4.设x∈R,若a<lg(x－3+x+7)恒成立，则（　　）

A.a≥1　　　　　　　　　　　　 B.a>1　　　　　　　　　　　　　 C.0<a≤1　　　　　　　　　　　　　　D.a<1

考查对数函数性质及绝对值不等式.

【解析】 令t=x－3+x+7,∴x∈R,∴t_min=10

y=lgt≥lg10=1,故a<1

【答案】 D

5.设有两个命题①关于x的不等式x²+2ax+4>0对于一切x∈R恒成立，②函数f(x)=－(5－2a)^x是减函数，若此二命题有且只有一个为真命题，则实数a的范围是（　　）

A.(－2,2)　　　　　　　　　　　　　　B.(－∞,2)　　　　　　　　　　C.(－∞,－2)　　　　　　　　D.(－∞,－2］

考查二次函数性质及逻辑推理能力.

【解析】 ①等价于Δ=（2a)²－16<0－2<a<2

②等价于5－2a>1a<2

①②有且只有一个为真，∴a∈(－∞,－2］

【答案】 D

6.设函数f(x)=f()lgx+1,则f(10)值为（　　）

A.1　　　　　　　　　　　　　　　B.－1　　　　　　　　　　　　　 C.10　　　　　　　　　　　　　　　　　 D.

考查对数性质及函数对应法则理解.

【解析】 ∵f(x)=f()lgx+1,∴f()=f(x)lg+1

∴f(10)=f()lg10+1,且f()=f(10)lg+1

解得f(10)=1.

【答案】 A

7.已知函数y=f(x)的反函数为f^－1(x)=2^x+1,则f(1)等于（　　）

A.0　　　　　　　　　　　　　　　B.1　　　　　　　　　　　　　　　C.－1　　　　　　　　　　　　　 D.4

考查反函数意义.

【解析】 令f(1)=x,则f^－1(x)=1,令2^x+1=1,∴x=－1

【答案】 C

8.若定义在区间（－1，0）内的函数f(x)=log_2a(x+1)满足f(x)>0,则a的取值范围是（　　）

A.(0,)　　　　　　　　　　　 B.(0,　　　　　　　　　　　 C.(,+∞)　　　　　　　　　 D.(0,+∞)

考查对数函数的单调性.

【解析】 f(x)=log_2a(x+1)>0=log_2a1

∵x∈(－1,0),∴x+1<1,

∴0<2a<1,即0<a<

【答案】 A

9.已知函数y=f(2^x)定义域为［1，2］,则y=f(log₂x)的定义域为（　　）

A.［1，2］　　　　　　　　　B.［4，16］　　　　　　　　C.［０，1］　　　　　　　　D.（－∞,0］

考查函数定义域的理解.

【解析】 由1≤x≤22≤2^x≤4,

∴y=f(x)定义域为［2，4］

由2≤log₂x≤4,得4≤x≤16

【答案】 B

10.已知f(x)=x²－bx+c,且f(0)=3,f(1+x)=f(1－x),则有（　　）

A.f(b^x)≥f(c^x)　　　　　　　　　　　　　　　　　　　　　　　　　 B.f(b^x)≤f(c^x)

C.f(b^x)<f(c^x)　　　　　　　　　　　　　　　　　　　　　　　　　　D.f(b^x)、f(c^x)大小不确定

考查二次函数及函数单调性.

【解析】 由f(0)=3c=3,

由f(1+x)=f(1－x)知对称轴为x=1,∴b=2

①x=0,2^x=3^x,∴f(2^x)=f(3^x)

②x>0,1<2^x<3^x,∴f(2^x)<f(3^x)

③x<0,1>2^x>3^x,∴f(2^x)<f(3^x)

【答案】 B

第Ⅱ卷(非选择题　共70分)

二、填空题(本大题共4小题，每小题4分，共16分)

11.方程log₂(2－2^x)+x+99=0的两个解的和是______.

考查对数运算.

【解析】 由原式变形得2－2^x=

设2^x=y,变形得:2⁹⁹y²－2¹⁰⁰y+1=0y₁y₂=2^－99=2

∴x₁+x₂=－99

【答案】 －99

12.当x∈(1,2)，不等式(x－1)²<log_ax,则a的取值范围是_____________.

考查对数函数图象及数形结合思想.

【解析】 考查两函数y=(x－1)²及y=log_ax图象可知a∈(1,2］

【答案】 (1,2］

13.若不等式3>()^x+1对一切实数x恒成立，则实数a的取值范围为______.

考查指数函数单调性及化归能力.

【解析】 由题意：x²－2ax>－x－1恒成立

即x²－(2a－1)x+1>0恒成立

故Δ=（2a－1）²－4<0－<a<

【答案】 －<a<

14.f(x)=，则f(x)值域为______.

考查分段函数值域.

【解析】 x∈(－∞,1］时,x－1≤0,0<3^x－1≤1,

∴－2<f(x)≤－1

x∈(1,+∞)时，1－x<0,0<3^1－x<1,∴－2<f(x)<－1

∴f(x)值域为(－2,－1］

【答案】 (－2,－1］

三、解答题（本大题共5小题，共54分.解答应写出文字说明、证明过程或演算步骤）

15.（本小题满分8分）已知函数f(x)=log²x－logx+5,x∈［2,4］，求f(x)的最大值及最小值.

考查函数最值及对数函数性质.

【解】 令t=logx,∵x∈［2,4］,t=logx在定义域递减有

log4<logx<log2，∴t∈［－1,－］

∴f(t)=t²－t+5=(t－)²+,t∈［－1,－］

∴当t=－时，f(x)取最小值

当t=－1时，f(x)取最大值7.

16.（本小题满分10分）已知f(x)=lg.

(1)求函数定义域.

（2）求f^－1(lg2).

考查函数性质，互为反函数的函数间关系.

【解】 （1）由>0,得－1<x<1

∴函数f(x)的定义域为{x－1<x<1}

(2)由lg=lg2=2x=－

∴f^－1(lg2)=－

17.(本小题满分12分)已知函数f(x)=(a^x－a^－x)(a>0且a≠1)是R上的增函数，求a的取值范围.

考查指数函数性质.

【解】 f(x)的定义域为R，设x₁、x₂∈R,且x₁<x₂

则f(x₂)－f(x₁)= (a－a－a+a)

=(a－a)(1+)

由于a>0，且a≠1,∴1+>0

∵f(x)为增函数，则(a²－2)( a－a)>0

于是有，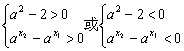

解得a>或0<a<1

18.(本小题满分12分)设函数f(x)=lgx,若0<a<b,且f(a)>f(b),证明：ab<1.

考查对数函数性质、分类讨论思想.

【解】 由题设，显然a、b不能同在（1，+∞)

否则，f(x)=lgx,且a<b时，f(a)<f(b)与已知矛盾

由0<a<b可知，必有0<a<1

①当0<b<1时，

∵0<a<1,0<b<1,∴0<ab<1

②当b>1时，∵0<a<1

∴f(a)=lga=－lga,f(b)=lgb=lgb

由f(a)>f(b),得－lga>lgb，即>b,∴ab<1

由①②可知ab<1

19.（本小题满分12分）某种细菌每隔两小时分裂一次，（每一个细菌分裂成两个，分裂所须时间忽略不计），研究开始时有两个细菌，在研究过程中不断进行分裂，细菌总数y是研究时间t的函数，记作y=f(t).

（1）写出函数y=f(t)的定义域和值域.

（2）在所给坐标系中画出y=f(t)(0≤t<6)的图象.

（3）写出研究进行到n小时（n≥0，n∈Z)时，细菌的总数有多少个（用关于n的式子表示）？

考查函数应用及分析解决问题能力.

【解】 （1）y=f(t)定义域为t∈［0,+∞),

值域为{yy=2ⁿ,n∈N^*}

（2）0≤t<6时，为一分段函数

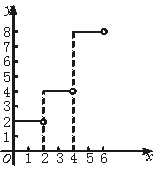y=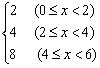

图象如图

（3）n为偶数时，y=2

n为奇数时，y=2

∴y=