“角的概念的推广”典型例题分析
例1 在 
～ 
间，找出与下列各角终边相同的角，并指出它是哪个象限的角。
（1） 
（2） 
（3） 
解：（1）∵ 
∴ 的角与 
的角的终边相同，它是第一象限的角。
（2）∵ 
∴ 的角与 
的角的终边相同，它是第四象限的角。
（3）∵ 
，
∴ 的角与 
的角终边相同，它是第二象限的角。
例2 写出与下列各角终边相同的角的集合T，并把T中在 
～ 
间的角写出来：
（1） 
；
（2）－ ；
（3） 
解：（1） 
T中在 ～ 间的角是：
，
（2） 
T在 ～ 间的角是：
（3） 
T在 ～ 间的角是：
，
，
例3 写出终边落在直线 
上的角的集合。
分析指导 从 ～ 间满足条件的角入手。
解: 在 ～ 间，满足条件的角是 
和 
，所以，终边落在 上的角的集合为
说明 本题易错解为 
这是思维不周密的具体表现。
例4 如果角 
与角 
具有同一条终边，角 
与角 
具有同一条终边，那么 与 间的关系是（ ）
A． 
B． 
C． 
D． 
分析指导 利用终边相同角的表示，分别建立 与 
， 与 的关系式，由此寻找 与 间的关系，对照选择。
解: 依题意， 
（ 
），
（ 
），那么
∵ 
、 
是整数， 
也是整数，用 
表示，
∴ 
故选D。
说明 此题易错选B。误认为 
， 
，故 
例5（1）设 是第二象限角，那么 
是第几象限角？
（2）设 是第一象限角，那么 
是第几象限角？
解：（1）∵ 是第二象限角，
∴
，
∴ 
当 
是偶数（例如 
）时， 是第一象限角；当 是奇数（例如 
，1，－1）时， 是第三象限角。见图1中的阴影部分。
（2）∵ 是第一象限角，
∴ 
，
∴ 
当 时， 
，
当 
时， 
，
当 
时， 
。
上述三种情况见图2中的阴影部分， 分别在第一、第二、第三象限。
不难得知，对于任何整数 ， 
也在上述三个象限中。
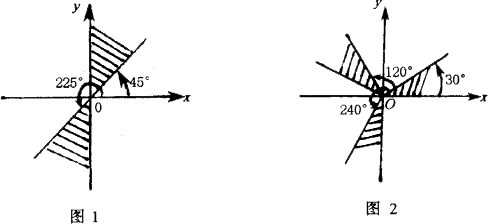
点拨：请同学们思考：图1与图2中， 与 所在象限有何特点？你是否可以找出某种规律来。
“弧度制”典型例题分析
例1 若 是第四象限角，则 
是（ ）
A．第一象限角 B．第二象限角
C．第三象限角 D．第四象限角
分析指导 从象限角的表示入手。
解: 若 是第四象限角，则
，于是
，从而有
，
所以， 在第三象限，故选C。
说明 考虑到选择题的特点，可赋特值检验，如取 
，则 
在第三象限。
例2 若集合 
， 
，求 
分析指导 从集合交集的定义出发，可得关于 的不等式，由 
，确定 的整数解，从而确定交集的元素即可．
解: 由交集定义，知
，即 
，
∴ 
由 ，知 
当 
时，
故 
说明 要逐步习惯在弧度制下进行运算。
例3 某种蒸汽机上的飞轮的半径为 
，每分钟按逆时针方向旋转250圈，求：
（1）飞轮每秒钟转过的弧度数；
（2）轮周上的一点每秒钟经过的弧长。
解：（1）飞轮每秒钟转过的弧度数是
（2）轮周上的一点每秒钟经过的弧长为
（或 
）
例4 在半径等于12 
的圆中，一扇形的弧含有 
角，求这个扇形的周长和面积（ 
取 
，计算结果保留小数点后两位）。
解： 的角的弧度数是 
，因此扇形弧长为
，
∴扇形周长为
扇形面积为：
例5 已知扇形的周长为30 ，当它的半径和圆心角各取什么值时，才能使扇形面积最大？最大面积是多少？
分析指导 根据题设，利用扇形的面积公式，建立面积关于半径的函数关系，即可转化为函数的最值问题处理。
解: 设扇形的圆心角为 ，半径为 
，面积为S，弧长为 
，则有
，即 
。
从而 
，
所以当 
时， 
，此时
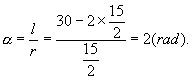
说明 本题即为弧度制的一个应用，它充分体现了弧度制下公式的特点，运算简捷明快。