提高测试一
1．两个等差数列2，5，8，…，197和2，7，12，…，197，中相同的数之和是（）
（A） 1196； （B）1391； （C）1393； （D）1169
答案：C
2．已知
是各项为正数的等比数列，
，那么
为（）
（A） 5； （B）10； （C）15； （D）20
答案：A
3．已知等差数列中，
，则n等于（）
（A） 38； （B）20； （C）19； （D）10
答案：D
4．两个等差数列，它们的前n项和之比为
，则这两个数列的第九项的比是_________
（答案：8∶3）
5．在数列中，
，则
______________。
（答案：
）
6．已知数列1，
，
，…， 
，…
，则此数列的前n项和
________________．
（答案：
）
7．已知数列中，Sn 是它的前n项和，且
．
（1）设
，求证数列
是等比数列；
（2）设
，求证数列
是等差数列
（答案： 7．（1）由题意，得
，
即
，变形得
，
即
，再由已知，
（2）由
，得
，又如，故
）
8．已知等差数列的首项为
，公差
．
（1）若
，求k的值；
（2）设的前n项和为Sn
，试问数列
是否存在相同的两项，若存在，求出这样的两项，若不存在，说明理由．
（答案：（1）k=10，（2）不存在；）
（点评：（1）易知
，令
，则
，即前6项的正数，从第7项开始为负数．
∴
.
解得
（舍）
（2）假设存在
，使
．则可以推出
，对于
，此式不可被成立，故
不存在相同的两次．）
9．已知数列的通项公式，
，问n取何值时，an 取最大值．
（答案：n=8或9时，an 最大；）
（点评：方法一：不妨设
最大，则
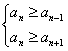，由此解得n=8或9
方法二：先分析的单调性．
，再时n分三类讨论，即
时；
时，an增函数；
时，an是减函数，进而得出结论．）
10．某企业为筹划资金A元，以年利率r每年度利计息借款，在当年初借入，前m年内不还款，从m+1年度开始每年以一定的金额a元偿还，但在后续的n年间要将借款本利和全部还清，求a
（答案：
（元）
点评：从借款到还清需
个年份，故A元的本利和是
元，而偿还金额的本利和是
故 
，解得 ）