同步训练----同角三角函数、诱导公式

同步训练----同角三角函数、诱导公式

一、选择题

1、若，则m=（ ）

A．0　　　　　　　　　　　　　　　　B．8

C．0或8　　　　　　　　　　　　　　D．3<m<9

2、已知，则sinα－ cosα= （　）

A．　　　　　　　　　　　　　　B．－

C．－　　　　　　　　　　　　　D．

3、已知（ ）

A．1 　　　　　　　　　　　　　　　B．2

C．　　　　　　　　　　　　　　D．

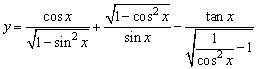4、函数的值是（ ）

A．{－1，1，3}　　　　　　　　　　B．{－3，1，－1}

C．{1，3}　　　　　　　　　　　　　D．{－3，1}

5、已知α是三角形的一个内角，且，则这个三角形的形状是（ ）

A．锐角三角形　　　　　　　　　　　B．钝角三角形

C．不等腰的直角三角形　　　　　　　D．等腰直角三角形

6、设则(tan⁴α＋tan²α)·cos²α·cot³α=（ ）

A．4　　　　　　　　　　　　　　　B．－4

C．　　　　　　　　　　　　　　　D．－

7、若，则sin(2π＋α)=（ ）

A．　　　　　　　　　　　　　　　B．±

C．　　　　　　　　　　　　　　D．－

8、已知（k∈Z），则A的值构成集合是（ ）

A．{1，－1，2，－2}　　　　　　　　B．{－1，1}

C．{2，－2}　　　　　　　　　　　　D．{1，－1，0，2，－2}

9、已知=（ ）

A．－5　　　　　　　　　　　　　　B．5

C．±5　　　　　　　　　　　　　　D．不确定

10、将角α的终边顺时针旋转，则它与以原点为圆心，1为半径的单位圆的交点的坐标是（ ）

A．（cosα，sinα）　　　　　　　B．（cosα，－sinα）

C．（sinα，－cosα）　　　　　　D．（sinα，cosα）

二、 填空题

11、已知tanα＋cotα=2，则tan²α＋cot²α=___________.

12、已知f(x)=x²＋4x，且f(2cosθ－1)=m，则m的最小值是___________.

三、解答题

13、已知sinθ＋cosθ=，θ∈（0，π），求①tanθ，②sinθ－cosθ，③sin³θ＋cos³θ.

14、设k∈Z，化简.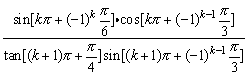

15、已知，求证：

.

答案：一、1----5CCABB　6----10DDCBC

1、由平方关系sin²α＋cos²α=1可解得m=0或8.

　　2、把已知条件两边平方即得。

　　3、由已知可解得，要求的式子可化为

　　　　

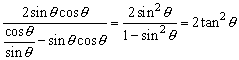
　　4、，然后分象限讨论.

　　5、由，故sinα>0，cosα＜0，即α为钝角.

　　6、原式=tan²α(tan²α＋1)·cos²α·cot³α=sec²α·cos²α·cotα=cotα.

　　7、

　　8、k为偶数时，

　　　k为奇数时，.

　　9、

　　10、设交点为P，则P.

　 　　　

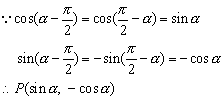
二、11、2　　　提示：： tan²α＋cot²α=(tanα＋cotα)²－2=2²－2=2.

12、－4 　　　 提示：m=(2cosθ－1)²＋4(2cosθ－1)=(2cosθ＋1)²－4.

　当 cosθ=－时，m最小为－4.

三、13、解：由 sinθ＋cosθ=平方得sinθcosθ=－<0.

∵ θ∈（0，π），∴ sinθ>0，cosθ<0，

由 (sinθ－cosθ)²=1－2sinθcosθ得

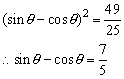
联合 sinθ＋cosθ=与sinθ－cosθ=，解得.

故.

14、解：k为偶数时，原式=.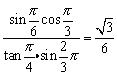

k为奇数时，原式=.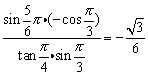

15、证明：由已知条件得：

　

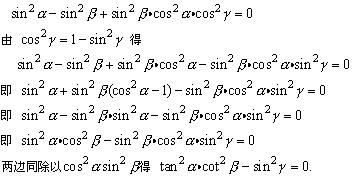
　　　故命题得证 .