线段的定比分点

第十教时

教材：线段的定比分点

目的：要求学生理解点P分有向线段所成的比λ的含义和有向线段的定比分点公式，并能应用解题。

过程：一、复习：1．向量的加减，实数与向量积的运算法则

　　　　　　　　　　　　　　　  2．向量的坐标运算

　　二、提出问题：线段的定比分点

1．线段的定比分点及λ

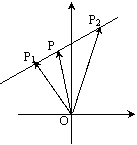
　　　　 　 P₁, P₂是直线l上的两点，P是l上不同于P₁, P₂的任一点，存在实数λ，

使　=λ　　　　λ叫做点P分所成的比，有三种情况：

λ>0(内分)　　　　　  　　 (外分) λ<0 (λ<-1)　　　　 ( 外分)λ<0　(-1<λ<0)

2．定比分点公式的获得：

　　　　　　　　　　　　　　　　 　　　　　　　　　 设=λ　点P₁, P, P₂坐标为(x₁,y₁) (x,y) (x₂,y₂)

　　　　　　　　　　　　　　　  　　　　　　　　　 由向量的坐标运算

　　　　　　　　　　　　　　　　　　　　　　　　　　　　  =(x-x₁,y-y₁)　　 =( x₂-x₁, y₂-y₁)

　　　　　　  　　　　　　　　　　　　　　　　　　 ∵=λ　　　 (x-x₁,y-y₁) =λ( x₂-x₁, y₂-y₁)

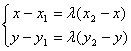
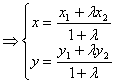　　　　　　　  ∴　定比分点坐标公式

3．中点公式：若P是中点时，λ=1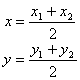　

4．注意几个问题：1° λ是关键，λ>0内分　λ<0外分　 λ¹-1

　　　　　　　　　 　　　　　　　　　　　　　若P与P₁重合，λ=0 　　　　P与P₂重合　　λ不存在

　　　　　  2° 中点公式是定比分点公式的特例

3° 始点终点很重要，如P分的定比λ=　则P分的定比λ=2

4° 公式：如 x₁, x₂, x, λ 知三求一

三、例题：例一　 (P114例一)　知三求一

　　　　　  例二 (P114例二)　 △重心公式

例三　若P分有向线段的比为，则A分所成比为（作示意图）

例四　过点P₁(2, 3),　P₂(6, -1)的直线上有一点，使 P₁P: PP₂=3, 求P点坐标

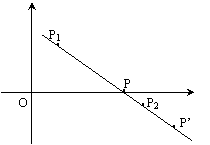　　　　　　　　　　　　　　　  　　　　　　　　　　　　　　 解：当P内分时 λ=3

　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　　　 当P外分时λ=-3

当λ=3得P(5,0)

当λ=-3得P(8,-3)

例五　△ABC顶点A(1, 1), B(-2, 10), C(3, 7)　ÐBAC平分线交BC边于D,　

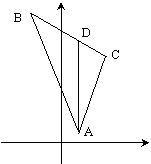求D点坐标

解：∵AD平分角ÐBAC

AC=

AB=

∴D分向量所成比λ=

设D点坐标(x, y)　则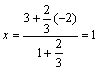　　　　

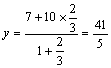
∴D点坐标为：(1,)

四、小结：定比分点公式，中点公式

五、作业：P115-116 练习　　 习题5.5