向量的加法与减法练习
基础卷（15分钟）
一、选择题
1．下列命题：
（1）如果非零向量
与
的方向相同或相反，那么，
的方向必与，之一的方向相同。
（2）△ABC中，必有
（3）若，则A，B，C为一个三角形的三个顶点。
（4）若，均为非零向量，则
与
一定相等。
其中真命题的个数为（ ）
A．0 B．1
C．2 D．3
2．给出下列3个向量等式：
（1）
（2）
（3）
。其中正确的个数是（ ）
A．0 B．1
C．2 D．3
3．在△ABC中，设
（ ）
A．
B．
C．
D．
4．已知ABCD是平行四边形，O为平面上任一点。设
，则（ ）
A．
B．
C．
D．
二、填空题
5．
。
6．（1）
；
（2）
。
提高卷（30分钟）
一、选择题
1．有下列3个不等式
（1）
（2）
（3）
其中正确的个数是（ ）
A．0 B．1
C．2 D．3
2．化简以下各式：
（1）
；（2）
；（3）
；（4）
。结果为零的向量的个数是（ ）
A．1 B．2
C．3 D．4
3．已知
，
，则
的取值范围是（ ）
A．[3，17]
B．（3，17）
C．[3，10]
D．（3，10）
4．下列命题中，正确的是（ ）
A．单位向量都共线
B．
C．若
，则
D．
且
5．已知一点O到平行四边形ABCD的3个顶点A，B，C的向量分别为，，
，则向量
等于（ ）
A．
B．
C．
D．
6．在平行四边形ABCD中，若
，则必有（ ）
A．
B．
或
C．ABCD是矩形
D．ABCD是正方形
7．若O是△ABC内一点，
，则O是△ABC的（ ）
A．内心
B．外心
C．重心
D．垂心
二、填空题
8．△ABC中，
，则
。
9．向量，满足
，
，则的最大值为：______，的最小值为：_____。
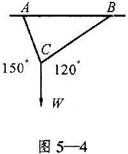
10．如图5—4，用两根绳子把重10kg的物体W吊在水平杆子AB上，∠ACW=150°，∠BCW=120°，则A和B处所受力的大小（绳子的重量忽略不计）分别是_______。
三、解答题
11．一辆汽车向东行驶30km，然后改变方向向北行驶30km，求汽车行驶的路程及两次位移的和。
12．设表示，“向北走20km，”表示“向南走10km”， 表示“向东走20km”， 
表示“向西走10km”，说明下列向量的意义：
（1）
；（2）
；（3）
；（4）
13．某人从A点出发向东走100m，到达B点， 然后改变方向向西北走200m，到C点，最后向西走100m到达D点，求
的值。
参考答案
基础卷
一、
1．B2．B3．B4．B
二、
5．
，
6．
，
[解题点拨]
1．命题
（1）中可能的零向量，其方向是任意的；
（3）中：A、B、C可能共线；
（4）中：只有与同向时，才有=，否则有<
4．
由
6．
（1）向量的加法满足交换律，故原式可化为
（2）
解法1（将向量减法转化为加法进行化简）原式=
解法2（利用
进行化简）原式
=
解法3：原式=
（本解法是利用
D进行化简的，其中O为平面内任意一点）
提高卷
一、
1．D2．C3．A4．B5．B6．C7．C
二、
8．
9．10，2；
10．
，5kg。
三、
11．汽车行驶的路程为60km，两次位移和的大小为
，方向是东偏北45°
12．（1）表示向北走40km；（2）表示向北走20 km；再向南走10km，（3）向北走20km再向西走10km，再向北走20km；（4）向南走10km，向东走20km；再向西走10km。
13．200m
[解题点拨]
2．（3）中
3．
而
（当
反向时取等号）
（
同向时取等号）即
6．
分别代表
ABCD的一条对角线。
7．设M为AB边的中点，利用关系
进行判断。
10．此题涉及物理学中力的合成与分解，由两根绳子拉力的合力大小等于物体重力的大小，利用向量加法的平行四边形法则予以解决。
13．ABCD构成一平行四边行，故
。