第三教时
教材:向量的减法
目的:要求学生掌握向量减法的意义与几何运算,并清楚向量减法与加法的关系。
过程:
一、复习:向量加法的法则:三角形法则与平行四边形法则
 向量加法的运算定律:
向量加法的运算定律:
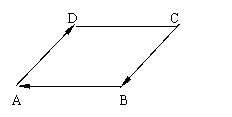
例:在四边形中,![]()
![]()
解:![]()
二、 提出课题:向量的减法
1.用“相反向量”定义向量的减法
1°“相反向量”的定义:与a长度相同、方向相反的向量。记作 -a
2°规定:零向量的相反向量仍是零向量。-(-a) = a
任一向量与它的相反向量的和是零向量。a + (-a) = 0
如果a、b互为相反向量,则a = -b, b = -a, a + b = 0
3°向量减法的定义:向量a加上的b相反向量,叫做a与b的差。
即:a - b = a + (-b) 求两个向量差的运算叫做向量的减法。
2.用加法的逆运算定义向量的减法:
向量的减法是向量加法的逆运算:
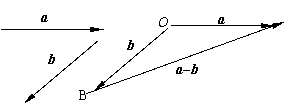 若b + x
= a,则x叫做a与b的差,记作a - b
若b + x
= a,则x叫做a与b的差,记作a - b
3.求作差向量:已知向量a、b,求作向量
∵(a-b) + b = a + (-b) + b = a + 0 = a
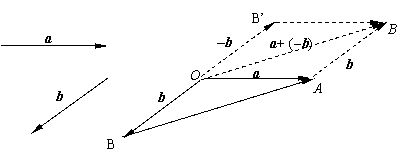
作法:在平面内取一点O,
作![]() = a,
= a, ![]() = b
= b
则![]() = a - b
= a - b
即a - b可以表示为从向量b的终点指向向量a的终点的向量。
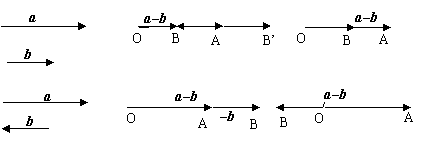
注意:1°![]() 表示a - b。强调:差向量“箭头”指向被减数
表示a - b。强调:差向量“箭头”指向被减数
2°用“相反向量”定义法作差向量,a - b = a + (-b)
显然,此法作图较繁,但最后作图可统一。
4. a∥b∥c
a - b = a
+ (-b) a - b
a∥b∥c
a - b = a
+ (-b) a - b
三、例题:
例一、(P101 例三)已知向量a、b、c、d,求作向量a-b、c-d。
解:在平面上取一点O,作![]() = a,
= a, ![]() = b,
= b, ![]() = c,
= c, ![]() = d,
= d,
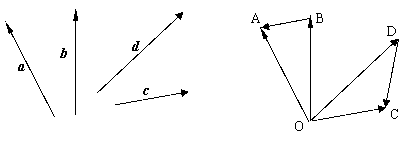 作
作![]() ,
, ![]() , 则
, 则![]() = a-b,
= a-b, ![]() = c-d
= c-d
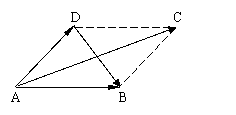 |
例二、平行四边形中,,用表示向量,
解:由平行四边形法则得:
![]() = a + b,
= a + b, ![]() =
= ![]() = a-b
= a-b
变式一:当a, b满足什么条件时,a+b与a-b垂直?(a = b)
变式二:当a, b满足什么条件时,a+b = a-b?(a, b互相垂直)
![]() 变式三:a+b与a-b可能是相当向量吗?(不可能,∵ 对角线方向不同)
变式三:a+b与a-b可能是相当向量吗?(不可能,∵ 对角线方向不同)
四、小结:向量减法的定义、作图法
五、作业: P102 练习
P103 习题5.2 4—8