向量的坐标表示与坐标运算

第八教时

教材：向量的坐标表示与坐标运算

目的：要求学生理解平面向量的坐标的概念，较熟练地掌握平面向量的坐标运算。

过程：一、复习：1．复习向量相等的概念

　　　　　　　　　　　　　　　　　　　　　　　　  　　　自由向量　　　　　　　　　　　　　　　　　　　　　　　  =

　　　　　　　　　  　　　　 　 2．平面向量的基本定理（基底）　　=λ₁+λ₂

　　　　　　　　　　　　 其实质：同一平面内任一向量都可以表示为两个不共线向量的线性组合。

二、平面向量的坐标表示

1．在坐标系下，平面上任何一点都可用一对实数(坐标)来表示

问题：在坐标系下，向量是否可以用坐标来表示呢？

取x轴、y轴上两个单位向量, 作基底，则平面内作一向量=x+y，

记作：=(x, y)　称作向量的坐标

　　　　　　　　　　　　  　　　　 如：==(2, 2)　　　=(1, 0)

　　　　　　　　　　　　　　　　　　　　  ==(2, -1)　 =(0, 1)

　　　　　　　　　　　　　　　　　　　　  ==(1, -5)　　 =(0, 0)

2．注意：1°每一平面向量的坐标表示是唯一的；

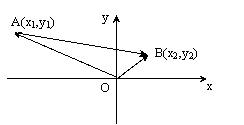
2°设A(x₁, y₁)　 B(x₂, y₂)　则=(x₂-x₁, y₂-y₁)

3°两个向量相等的充要条件是两个向量坐标相等。

　　　　3．例一：(P109)略

三、平面向量的坐标运算

1．问题：1°已知(x₁, y₁)　 (x₂, y₂)　 求+，-的坐标

2°已知(x, y)和实数λ,　 求λ的坐标

2．解：+=(x₁+y₁)+( x₂+y₂)=(x₁+ x₂) + (y₁+y₂)

即：+=(x₁+ x₂,　y₁+y₂)

同理：-=(x₁- x₂,  y₁-y₂)

3．结论：两个向量和与差的坐标分别等于这两个向量相应坐标的和与差。

同理可得：一个向量的坐标等于表示此向量的有向线段终点的坐标减去始点的坐标。

用减法法则：　　

∵=-=( x_2, y₂) - (x₁,　y₁)

= (x₂- x₁, y₂- y₁)

 4．实数与向量积的坐标运算：已知=(x, y)　 实数λ

则λ=λ(x+y)=λx+λy

∴λ=(λx, λy)

结论：实数与向量的积的坐标，等于用这个实数乘原来的向量相应的坐标。

四、例二（P110例二）

例三（P111例三）

例四（P145例一）已知三个力 (3, 4),　(2, -5), (x, y)的合力++=

求的坐标。

解：由题设++=　 得：(3, 4)+ (2, -5)+(x, y)=(0, 0)

即：　　∴　　∴(-5,1)

例五、已知平面上三点的坐标分别为A(-2, 1), B(-1, 3), C(3, 4)，求点D的坐标使这四点构成平行四边形四个顶点。

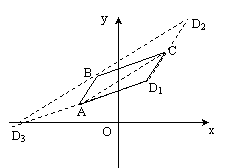解：当平行四边形为ABCD时，

仿例三得：D₁=(2, 2)

当平行四边形为ACDB时，

仿例三得：D₂=(4, 6)

当平行四边形为DACB时，

仿上得：D₃=(-6, 0)

五、小结：1．向量的坐标概念　　　　　　　　 2．向量运算

六、作业：P112 练习 1—3　　　　　　　  习题5.4 　1—6