正弦、余弦的诱导公式
基础练习
1．求下列三角函数值：
（1）sin（－120°）； （2）cos（－240°）； （3）tan（－135°）；
（4）
；
（5）
（6）
．
2．求下列三角函数值：
（1）sin（－2460°）； （2）cos840°； （3）tan（－2025°）
（4）
；
（5）
； （6）
．
3．将下列各值化为锐角的三角函数值：
（1）sin4321°； （2）
； （3）
； （4）cos2001°．
4．下列各式的值等于－sinA的是（ ）．
A．sin（p－A） B．sin（k·360°－A），k∈Z
C．sin（k·360°＋A），k∈Z D．－sin（－A）
5．如果a＋b＝180°，那么下列等式中成立的是（ ）．
A．sina ＝－sinb B．cosa＝cosb
C．sina ＝sinb D．cos（a ＋b ）＝1
6．函数式
化简的结果是（ ）．
A．sin1－cos1 B．sin1＋cos1
C．±（sin1－cos1） D．cos1－sin1
7．已知
，求
的值．
8．若（－4，3）是角a 终边上一点，则
的值为_______．
综合练习
1．求下列三角函数值：
（1）
；
（2）sin（－1590°）； （3）cos（－1260°）；
（4）
；
（5）sin（－542°）； （6）
．
2．设A、B、C是某三角形的三个内角，给出下列四个命题：
（1）sin（A＋B）＝sinC；
（2）cos（B＋C）＝cosA；
（3）tan（A＋C）＝tanB；
（4）A＋B＋C＝p ．
其中正确的命题是（ ）．
A．（1）（2） B．（2）（3） C．（3）（4） D．（1）（4）
3．a 是第三象限的角，则下列各式中其值恒正的是（ ）．
A．sina－cos（p－a） B．－tana－cos（p＋a）
C．tan（a－2p）＋sin（2p－a） D．－tan（4p＋a）＋sina
4．
的值是（ ）．
A．
B．
C．
D．
5．当
时，求cos（―a―5p）tan（3p＋a）sin（a－7p）－1的值．
6．已知f（x）＝
，则下列等式成立的是（ ）．
A．
B．
C．
D．
7．化简：（1）
（k∈Z）；
（2）
．
8．化sin（75p＋a）（a 为钝角）为锐角的三角函数为________．
9．已知
，（其中a、b、a、b都是常数），则asin（2002p＋a）＋bcos（2002p＋b）的值为________．
10．已知
，则
的值为________．
拓展练习
1．
．
2．计算：
＋
＋…＋
＋
＋
＋
＋…＋
＋
．
3．化简：
＋
＋
＋…＋
，k∈Z．
4．已知q 是锐角，sin（－q ）和cos（－q ）是方程
（m是常数）的两个根，求sinq ＋cosq 的值．
5．设A、B、C、D是圆内接四边形ABCD的四个内角，求证：
（1）sinA＝sinC；
（2）cos（A＋B）＝cos（C＋D）；
（3）tan（A＋B＋C）＝－tanD．
6．设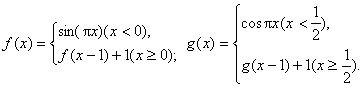
求
的值．
参考答案
基础练习
1．（1）
；（2）
；（3）1；（4）
；（5）
；（6）
．
2．（1）；（2）
；（3）－1；（4）；（5）；（6）
．
3.（1）sin1°；（2）
；（3）
；（4）－cos21°．
4．B 5．C 6．B．
7．
．由已知得
，
．
8．原式可化为
，由条件
，故所求值为
．
综合练习
1．（1）；（2）；（3）－1；（4）；（5）0.0349；（6）－0.2225．
2．D 3．C 4．A
5．
．化简
cos（－a－5p）tan（3p+ a）sin（a－7p）－1＝－cos2a． 6．B．
7．（1）当k＝2n（n∈Z）时，有原式
；当k＝2n＋1（n∈Z）时，原式
．
（2）原式＝
＝
＝
＝
＝－1．
8．－sin（p－a）．
9．－3．asin（2001p＋a）＋bcos（2001p+b）＝－asina－bcosb=3． ∴asin（2002p＋a）＋bcos（2002p＋b）＝asina+bcosb＝－3．
10．
．
．
拓展练习
1．原式
．
2．原式＝
．
3．原式＝（－sina＋sina）＋（－sina＋sina）＋…＋（－sina＋sina）＝0.
4．由已知
，即
，∴ 
，于是
．
，又q为锐角．∴
＝
．
5．由已知A＋C＝p，A＋B＋C＋D＝2p 得A＝p－C，则sinA＝sin（p－C）＝sinC，又A＋B＝2p－（C＋D），故cos（A＋B）＝cos[2p－（C＋D）]＝cos（C＋D）.tan（A＋B＋C）＝tan（2p－D）＝－tanD．
6．由已知
，
，
，
．故原式＝3．0