三角函数测试题

三角函数测试题

一．选择题（5分×12=60分）

1．tan300^o＋cot405^o的值为

A．1＋　　 B.1－　　  C.－1－　　  D.－1＋

2.令a=sin(π－1),b=sin2,c=cos1,则它们的大小顺序为

A.a>b>c　　　  B.b>a>c　　　 C.c>b>a　　　　 D.c>a>b

3.函数y=sin(－x)的递增区间是

A.[ 2kπ－π,2kπ＋](k Z)　　　　　　 B.[ 2kπ＋,2kπ＋](k Z) C.[2kπ＋,2kπ＋](k Z)　　　　　　　　 D.[2kπ－, 2kπ＋](k Z)

4.sin6^ocos24^osin78^ocos48^o的值等于

A.－　　　　B.　　　　  C.　　　　　 D.－

5.已知sinαcosα=且α(,),则cosα–sinα的值是

A.　　　　　 B.－　　　　C. 　　　　　D.－

6. 函数f(x)=cos(3x－θ)－sin(3x－θ)是偶函数,则θ等于

A. kπ　　　　 B. kπ＋　　C. kπ－　　 D. kπ＋

7. 已知点P(sinα－cosα,tanα)在第一象限,则在α [0,2π]内α的取值范围是

A.(, π) ∪（π, ）　　　　　　　  B. (,)∪(π, )

C. (, π) ∪ (,π)　　　　　　　 D.(,)∪(π, π)

8. 函数f(x)=cos（2x＋φ）的图像关于点（,0）中心对称的充要条件是

A. φ= ＋kπ(k Z)　　　　　　　　　　 B. φ= －＋2kπ(k Z)

C. φ=－＋kπ(k Z)　　　　　　　  　　D. φ= ＋2kπ(k Z)

9.如图正弦曲线对应的函数解析式是

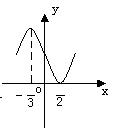　　A. y=sin（x＋）＋　　　　　　　　

　　B. y=sin（x＋）＋

C. y=3sin（12x＋）　　　　　　　　　　　 

D. y=sin（x＋）＋

10.下列四个函数中以π为最小正周期,且在区间（）上为减函数的是

A.y=cosx　　 B.y=2 sinx　　 C.y=（）^cotx D.y=-cosx

11.在平面直角坐标系中,已知A（cos80^o,sin80^o）、B（cos20^o,sin20^o）, 则｜AB｜的值是

A.　　　　 B.　　　　 C.　　　　　  D.1

12.函数f（x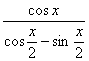）=的值域是

A.（-,）　　　　　　  B.[-,]

C. [ -,0) ∪(0,]　　  D. （-,0）∪（0,）

二.填空题（4分×4=16分）

13．已知 sinα– sinβ= a，cosα+cosβ=b，则cos（α+β）=　　　　　　　

14．已知sinx=，则 sin2（x－）=　　　　　　　　

15. f（x）是以5为周期的奇函数,　f（－3）=　4且cos α=, 则f（4cos2α）的值是　　　

16. 已知x[0, ],函数y=4sinxcosx+cos2x的值域是　　　　　　　

三角函数测试题

　　　　　　　　　　　

 班级　　　　 　　　 姓名　　　　　 　

一.　 选择题:

序号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二.填空题:

13.　 　　　　　　　 　　　　　　14.　　　　　　　 

15. 　　　　　　　 　　　　　　16.　　　　　　　 

 

三.解答题（12分×5+14分=74分）

17. 已知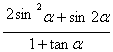=k（<α<）,试用k表示sinα－cosα的值.

18. 已知0<α<，cosα－sinα=－，求的值.

19. 求值:－＋64sin²20^o

20. 已知函数f（x）=5sinxcosx－5cos²x＋（x R）.

（1）　　　 求 f（x）的单调区间;

（2）　　　 求 f（x）图象的对称轴, 对称中心;

（3）　　　 函数f（x）的图象经过怎样的变化得到y=5sinx的图象

21. .在△ABC中,角A、B、C依次成等差数列,求cos²A＋cos²C的取值范围.

22. 已知函数y=2sinαcosα－sinα－cosα（0≤α≤π）.试问这个关于α的函数有没有最大值、最小值?若有,求出最值.

 

三角函数测试题参考答案

　　　　　　　　　　　　 

一.选择题:

序号	1	2	3	4	5	6	7	8	9	10	11	12
答案	B	B	B	C	B	D	B	A	B	B	D	A

二.填空题:

13.　 　　　　　 14.　2－

15. －4　　　　　　　　　 16.　[－1, 3 ]

 

三.解答题（12分×5+14分=74分）

17. 已知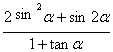=k（<α<）,试用k表示sinαcosα的值.

解：k===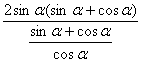2sinαcosα .

　　又<α< ,　∴sinα＞cosα　∴sinαcosα==

即sinαcosα= .

18. 已知0<α<，cosα－sinα=－，求的值.

解: ==

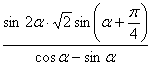=.　　　 　 由 cosα－sinα=－，两边平方得sin2α=.　

又cos（α+）=－, ∴cos（α+）=－.

而0<α< ,　∴<α+<,　∴sin（α+）=.　　∴原式==－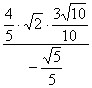

19.　　　　　 求值:－＋64sin²20⁰.

解:　原式=+64sin²20⁰

 =+64sin²20⁰

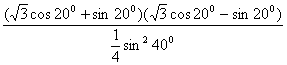　　　 =+64sin²20⁰　　 = 32cos40⁰ +32（1－cos40⁰）　 = 32 .

20. 已知函数f（x）=5sinxcosx－ 5cos²x＋（x R）.

（1）求 f（x）的单调区间;

（2）求 f（x）图象的对称轴, 对称中心;

（3） 函数f（x）的图象经过怎样的变化得到y=5sinx的图象.

解: f（x）=sin2x－5＋ = sin2x－cos2x = 5sin（2x－）.

（1）　　　 由2kπ－≤2x－≤2kπ＋

得[ kπ－, kπ＋], k Z为f（x）的单调增区间.

由2kπ＋≤2x－≤2kπ＋得[ kπ＋, kπ＋], k Z为f（x）的单调减区间.

（2）令2x－= kπ＋，得x= kπ＋，k Z为f（x）图象的对称轴方程.

令2x－= kπ，得x= kπ＋, k Z.　 故对称中心为（kπ＋,　0 ）, k Z.

（3）将y = 5sin（2x－）图象上每一点的横坐标扩大到原来的2倍,纵坐标不变,得到

y = 5sin（x－）.　 然后,将y=5sin（x－）图象上每一点向左平移个单位,纵坐标不变,即得到y=5sinx的图象.

21.　  在△ABC中,角A、B、C依次成等差数列,求cos²A＋cos²C的取值范围.

 解:∵ A、B、C成等差数列, ∴B=60^o, ∴C=120^o－A.

∴ cos²A＋cos²C= cos²A＋cos²（120^o－A）= cos²A＋（－cosA+sinA）²

= cos²A＋（cos²A＋sin²A－sinAcosA）=cos²A＋sin²A－ sin2A

= cos²A＋－ sin2A= cos2A－ sin2A　+1 =cos（2A+60^o）+1

∵0^o<A<120^o　 ∴60^o<2A+60^o<300^o　∴ －1≤cos（2A+60^o）＜

∴≤1+ cos（2A+60^o）＜ ,　 即cos²A＋cos²C的取值范围是[，）.

22. 已知函数y=2sinαcosα－sinα－cosα（0≤α≤π）.试问这个关于α的函数有没有最大值、

最小值？若有，求出最值.

解: 设u= sinα+cosα,则 sinαcosα=,　y=u²－u－1=（u－）²－.

又u= sinα+cosα=sin（α+）. ∵α [0,π]　　∴α+ [,π]

∴－≤ sin（α+）≤1　　∴－1≤u≤

对于y=（u－）²－，u [－1, ]有：u=时，y_min=-;　　u=－1时，y_max=1.