三角函数单元测试题二
一、选择题：本大题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的．
（1）
的值为（ ）．
A．
B．
C．
D．
（2）函数
的定义域是（ ）．
（A）
（B）
（C）
取
（D）
（3）已知
，
是第二象限角，且
，则
等于（ ）．
A．
B．
C．－7
D．7
（4）函数
的最小正周期是（ ）．
A．
B．
C．
D．
（5）（文）当
时，函数
的最大值为（ ）．
（A）0 （B）5 （C）
（D）3
（理）函数
的值域为（ ）．
A．
B．
C．
D．
（6）若
，则
的值为（ ）．
A．
B．
C．
D．
（7）设
，则
、
、
的大小是（ ）．
A．
B．
C．
D．
（（8）．函数
的单调递增区间是（ ）．
（A）
（B）
（C）
（D）
（9）函数
的图象可由函数
的图象向右平移（ ）个单位而得到．
（A）
（B）
（C）
（D）
（10）设
，那么
是函数
为奇函数的（ ）．
A．充分非必要条件
B．必要非充分条件
C．充分必要条件
D．既非充分也非必要条件
（11）如果
，那么
的值为（ ）．
A．
B．－ C．
D．－
（12）函数
的图象与函数
的图象在闭区间
上（ ）．
A．可能没有公共点 B．只有一个公共点
C．一定有两个公共点 D．至少有一个公点
二、填空题：本大题共4小题，每小题4分，共16分把答案填在题中横线上
（13）
中，
，那么这个三角形的最大角的度数为 ．
（14）已知
,那么
的值等于 ．
（15）函数
的图象的两条相邻的对称轴之间的距离为
，则
．
（16）是定义在R上的奇函数，且
对任意
成立，则
的值=
．
三、解答题：本大题共6小题，共74分解答应写出文字说明，证明过程和演算步骤
（17）（本小题满分12分）．
已知
，求
的值．
（18）（本小题满分12分）
设函数
满足
（Ⅰ）求、的值；
（Ⅱ）求使
成立的的取值集合．
（19）（本小题满分12分）
求函数
的最大值和最小值．
（20）（本小题满分12分）
在，角A、B、C的对边分别为、、，若
，
且
，求
的值．
（21）（本小题满分12分）
在中，
于D，作
，交AC于F，BC于E．求当x取什么值时，
的面积最大，并求这面积的最大值．
（22）（本小题满分14分）
已知
，求
的最大值．
单元测试题答案
一、选择题
（1）B （2）C （3）D （4）C （5）(文)B、（理）A （6）A （7）A （8）A （9）B （10）C （11）D （12）D
提示：
（3）由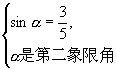
得
，又
（4）经变形，得
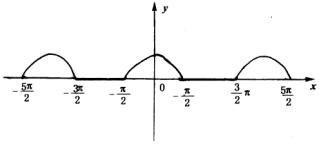
（5）（理）由
，根据反余弦函数的图象，可得函数的值域为
．
（6）由已知可得
且
（7）
（10）必要性显然，若，即
，
则
∴ 
是奇函数．
（11）令
，则
（12）取特例作研究，设
，则
结合图象作分析时，注意两函数相邻两个公共点间距离为，区间
的长度也为．
二、填空题：
（13）
（14）
（15）3 （16）0
提示：
（13）本题即
，求角C，可用余弦定理．
（15）本题即的最小正周期之半为
（16）易有
，又
，
故
三、解答题
（17）∵ ，
故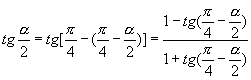
∴ 
，
∴ 
∴ 
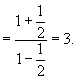
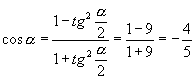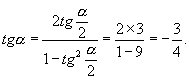
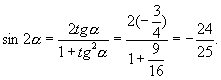
（18）（Ⅰ）由
，即
，故
又
，即
，故
（Ⅱ）
∴ ，即
∴ 
∴ 
∴ 所求的取值集合为
（１９）设
，则由
可得到
．
又
．故
，
可得
时，
的最大值为
；
时，的最小值为
.
（20）由
,
得 
，
∴ 
，∴
又，依正弦定理有
∴ 
，
即 
由此可得 
（２１）如图，设
，
（
均定值），
则在
，
中，分别可得
，
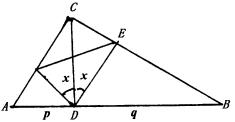
于是
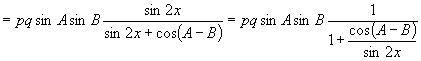
因此当
即
时，的最大面积为
.