三角函数单元测试题一
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)已知集合![]() ,
,
![]() ,那么集合M、P 的关系是(
).
,那么集合M、P 的关系是(
).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
(2)若![]() 是第二象限,则角
是第二象限,则角![]() 是( ).
是( ).
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
(3)![]() 的值为( ).
的值为( ).
A.![]() B.-
B.-![]() C.
C.![]() D.
D.![]()
(4)已知![]() 是第二象限角,且
是第二象限角,且![]() ,那么
,那么![]() 角所在的象限是( ).
角所在的象限是( ).
A.一 B.二 C.三 D.四
(5)![]() 的值为( ).
的值为( ).
A.0 B.![]() C.
C.![]() D.-
D.-![]()
(6)化简![]() 后可得到( ).
后可得到( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(7)如果![]() ,
,![]() ,那么
,那么![]() 等于( ).
等于( ).
(A)![]() (B)2 (C)3 (D)
(B)2 (C)3 (D)![]()
(8)若![]() ,化简
,化简![]() 得( ).
得( ).
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(9)已知![]() 那么点
那么点![]() 一定在( ).
一定在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(10)若![]() ,则
,则![]() 等于( ).
等于( ).
(A)![]() (B)0 (C)1 (D)
(B)0 (C)1 (D)![]()
(11)![]() 中,若
中,若![]() ,则
,则![]() 一定是( ).
一定是( ).
(A)正三角形 (B)锐角三角形
(C)钝角三角形 (D)直角三角形
(12)已知![]() 是第四象限角,
是第四象限角,![]() ,那么
,那么![]() 等于( ).
等于( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
(13)已知![]() 是第三象限角,且
是第三象限角,且![]() ,那么
,那么![]() 的值为___________.
的值为___________.
(14)已知![]() ,那么
,那么![]() 的值= .
的值= .
(15)若![]() ,则
,则![]() 的值为_______________.
的值为_______________.
(16)若![]() 与
与![]() 是关于
是关于![]() 的方程
的方程![]() 的两根,则实数
的两根,则实数![]() ,
,![]() 之间的关系是 (用等式表示).
之间的关系是 (用等式表示).
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程和演算步骤.
(17)(本小题满分12分)
求![]() 的值.
的值.
(18)(本小题满分12分)
已知![]() ,求
,求![]() 的值.
的值.
(19)(本小题满分12分)
求证: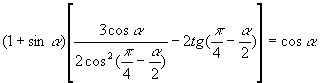
(20)(本小题满分12分)
在![]() 中,
中,![]() ,求
,求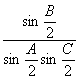 的值.
的值.
(21)(本小题满分12分)
已知圆内接四边形ABCD 的边长分别为![]() ,求四边形ABCD 的面积.
,求四边形ABCD 的面积.
(22)(本小题满分14分)
在![]() 中,如果
中,如果![]() ,求证
,求证![]() 是等边三角形.
是等边三角形.
答案与提示
一、选择题
(1)C (2)A (3)A (4)C (5)B (6)C (7)B (8)C(9)B
(10)B (11)C(12)A
提示:
(4)依已知![]() 是第一象限角或第三象限角,且
是第一象限角或第三象限角,且![]() .
.
(10)由已知得![]() ,
,![]()
![]() .
.
(11)若A为直角,则![]() ;若A为锐角,则
;若A为锐角,则![]() .
.
(12)由已知可得,![]() ,
,
故本题具有确定![]() 取值范围的隐含条件:
取值范围的隐含条件: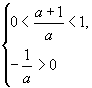 即
即![]() ,
,
于是![]()
二、填空题
(13)![]() (14)
(14)![]() (15)
(15)![]() (16)
(16)![]()
提示:
(13)因为![]()
![]()
![]() ,故由已知可得
,故由已知可得![]() ,又由
,又由![]() 是第三象限角,故
是第三象限角,故![]() ,于是
,于是![]() .
.
(14)![]() ,令
,令![]() ,而求
,而求
(15)由已知得![]() ,故
,故![]() ,再用万能公式求
,再用万能公式求![]() .
.
(16)依已知有![]() ,
,![]() ,
,
又![]()
三、解答题
(17)原式![]()
![]()
(18)由![]() ,即
,即![]() ,可解得
,可解得
![]() ,
,
于是![]() ,
,![]() ,故原式
,故原式![]() .
.
(19)左式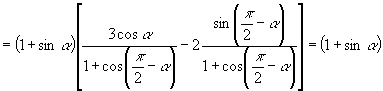
![]()
(20)由![]() ,
,
得![]() ,
,
由于![]() ,于是得
,于是得![]() ,
,
因此原式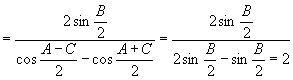 .
.
(21)如图,
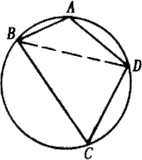
连结BD,
则四边形ABCD的面积![]()
![]()
∵ ![]() ,故
,故![]()
∴ ![]()
![]()
由余弦定理,在![]() 中,
中,
![]()
在![]() 中,同样有
中,同样有![]()
∴ ![]()
又![]() ,
,
于是可得 ![]()
∴ ![]()
(22)![]() ,故
,故![]()
![]() ,又
,又![]()
![]() ,
,
故![]() ,于是
,于是![]() ,因此
,因此![]() 为等边三角形.
为等边三角形.