三角函数的图象和性质一
1．函数y＝2sin(2x＋)得图象是
A.关于原点成中心对称图形 B.关于y轴成轴对称图形
C.关于点(，0)成中心对称图形 D.关于直线x＝成轴对称图形
2．已知函数
，则此函数是
A．周期为π的偶函数 B．周期为
的偶函数
C．周期为π的奇函数 D．周期为的奇函数
3．下列四个函数，同时具有性质：①最小正周期为π；②图象关于直线
对称的是
A．
B．
C．
D．
4 ．函数
是
A．最小正周期为2π的奇函数 B．最小正周期为2π的偶函数
C．最小正周期为π的奇函数 D．最小正周期为π的偶函数
5．函数f(x)=sin(ωx+
)cos(ωx+) (ω>0)以2为最小正周期，且能在x=2时取得最大值，则的一个值是（ ）
A．
B．
C．
D．
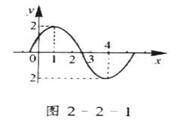6．如图2-2-1，给出函数y=f(x)=Asin(ωx+)图象的一段，则f（x）的表达式为
A．
B．
C．
D．
7．已知tgθ和
是方程
的两根，则p，q间的关系是
A．p-q+1=0 B．p+q+1=0 C．p+q-1=0 D．p-q-1=0
8．△ABC中，BC=a（a为正常数）且
，则顶点A的轨迹是
A．直线 B．椭圆
C．双曲线的一支（顶点除外） D．抛物线（顶点除外）
9．已知a，b，c分别是△ABC的三个内角A，B，C的对边。
（1）若△ABC的面积为
，C=2，A=60°，求a和b的值；
（2）若acosA=bcosB，试判断△ABC的形状，并证明。
10．求函数
的最小正周期。
11．19.已知函数f(x)=5+2
sinxcosx-6cos2x，求：
(1)f(x)的最小正周期和f(x)的最小值； (2)f(x)的单调递增区间.
三角函数的图象和性质二
1．函数
的单调递增区间是
A．[4kπ，（4k+2）π]（k∈Z） B．[4k，4k+2]（k∈Z）
C．[2kπ，（2k+2）π] （k∈Z） D．[2k，2k+2] （k∈Z）
2．函数
图象的两相邻对称轴之间的距离是
A．
B．π C．
D．
3．若函数y=f(x)的图象上每一点的纵坐标保持不变，横坐标伸长为原来的2倍，然后再将整个图象沿x轴向左平移个单位，沿y轴向下平移一个单位，得到的曲线与
的图象相同，则f(x)的表达式为
A．
B．
C．
D．
4．若f(x)sinx是周期为π的奇函数，则f（x）可以是
A．sinx B．cosx C．sin2x D．cos2x
5．△ABC的外接圆半径为R，a、b分别是∠A、∠B的对边，若
则∠C等于
A．30° B．45° C．135° D． 150°
6．函数
的图象上最高点与最低点的最近距离是_______。
7．若0≤α≤2π，且cosα≤sinα，则角α的取值范围是____________。
8．函数
的最大值为________，最小值为______________。
9．要得到y=cos2x的图象，只需把的图象向_ _ 平移__ __。
10．将函数
的图象按向量
平移，则平移后的图象所对应的函数解析式是 ．
11．已知函数
（1）求它的定义域值域和单调区间；（2）判断它的奇偶性（3）判断它的周期性
12．用五点法列表作出
的图象，并说明图象可由函数y=sinx的图象经过怎样的变换得到。
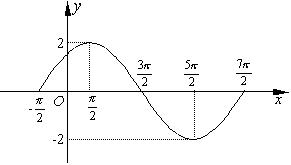13．已知函数f(x)＝Asin(ωx＋φ)(A＞0,ω＞0,x∈R)在一个周期内的图象如图所示，求直线y＝与函数f(x)图象的所有交点的坐标.