| 一、复习要点
三角函数的性质(包括三角公式)与图象是解答三角函数问题的知识基础;借助三角函数的图象来理解、掌握、运用三角函数的基本性质,是常用的复习方法.
三角函数的周期性、奇偶性、单调性、对称性、值域性质、关系性质(包括相等关系与不等关系)的判定与应用,是本节复习的重点;掌握好图形变换中,三角函数的图象、表达式及其性质的对应变化规律(要求能把这种规律迁移到一般函数理论中),是本节复习的又一重点,也是难点.
二、例题讲解
例1(1)如果α,β∈((π/2),π),且tgα<ctgβ,那么必有( ).
A.α<β
B.β<α
C.α+β<(3/2)π
D.α+β>(3/2)π
(1992年高考文科试题)
(2)满足arccos(1-x)≥arccosx的取值范围是( ).
A.[-1,-(1/2)]
B.[-(1/2),0]
C.[0,(1/2)]
D.[(1/22),1]
(1997年高考理科试题)
(3)已知点P(sinα-cosα,tgα)在第一象限,则在[0,2π)内α的取值范围是________. (1998年高考题)
讲解:(1)本题要用已知的正切函数tgα与余切函数ctgβ的大小关系,来推断角α与β的大小关系,回忆与这个问题紧密相关的基础知识与方法,若想到函数的单调性和利用单位圆作直观分析的方法,可理出如下推断方法: | 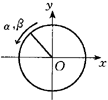
| | 图3-1 | 在单位圆的第二象限中,让角α、β沿逆时针方向旋转,则看到:tgα从-∞开始单调递增到0,而ctgβ从0开始单调递减向-∞;若α与β重合在第二象限的角平分线上,则tgα=ctgβ=-1.立知当α与β在第二象限的上半象限中任意变化,即α,β∈((π/2),(3π/4))时,总有tgα<ctgβ;而α,β∈((3π/4),π)时,总有tgα>ctgβ.从而由α,β∈((π/2),π),tgα<ctgβ,推出π<α+β<(3π/2).选C.
若想用解不等式的方法作推断,并在变形中巧用正切倍角公式,又得如下解法:
∵ α,β∈((π/2),π),
tgα<ctgβ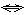 tgα<(1/tgβ) tgα<(1/tgβ)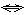 tgαtgβ>1 tgαtgβ>1
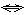 1-tgαtgβ<0 1-tgαtgβ<0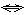 (tgα+tgβ)/tg(α+β))<0, (tgα+tgβ)/tg(α+β))<0,
∴ tgα<ctgβ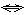 (tgα+tgβ)/tg(α+β))<0. (tgα+tgβ)/tg(α+β))<0.
∵ tgα+tgβ<0,
∴ tg(α+β)>0,并推得π<α+β<(3π/2).
故选C.
若考虑函数的单调性,由tgα<ctgβ,得
tgα<tg((3/2)π-β).
∵ α,β∈((π/2),π),∴ (3/2)π-β∈((π/2),π).
又y=tgx在((π/2),π)上是增函数,
∴ α<(3/2)π-β,故选C.
此题还可以用极限思想做推断:
当(π/2)<α<π,(π/2)<β<π,且α→(π/2),β→(π/2)时,有tgα→-∞,ctgβ→0.
∴总有tgα<ctgβ成立.可见A、B、D均不成立,故选C.
(2)本题是关于反余弦函数的简单不等式解集的判定问题.若想利用反余弦函数的图象来分析判定,则先想出或画出草图.由图可知,反余弦函数在定义域[-1,1]上单调递减,所以原不等式等价于 | 1-x≤x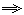 x≥(1/2) x≥(1/2) | 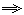 (1/2)≤x≤1. (1/2)≤x≤1.
| | -1≤x≤1, | 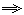 0≤x≤1 0≤x≤1
| | -1≤1-x≤1 | 故而选D. | 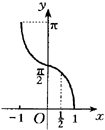
| | 图3-2 | 若能注意到,在x轴上x与1-x两点关于(1/2)点对称,则由图象立即看出x的取值范围是(1/2)≤x≤1.
若想利用特殊值法判定,则取x=-(1/2),可排除A、B;取x=0,可排除C.
(3)本题的条件是几何型的,而目标却是求变量α的取值范围,所以解答此题,应首先将几何型条件等价转化为不等式或不等式组,然后分析求解得出答案.现分析解答如下.
点P(sinα-cosα,tgα)在第一象限 | 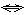 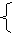
| sinα-cosα>0, |  
| sinα>cosα, | ① | | tgα>0 | tgα>0. | ② | 在单位圆中分析易知:满足不等式①的α为第一、三象限角平分线左上方半圆中的角;满足不等式②的α角为第一或第三象限中的角. | 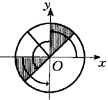
| | 图3-3 | 故取以上两个α的变化范围所对应的集合与区间[0,2π)的交集,即得α的取值范围是((π/4),(π/2))∪(π,(5π/4)).
例2 把函数y=sin(ωx+φ)(其中φ为锐角)的图象至少向右平移(π/8)或至少向左平移(3π/8),可使对应的函数成为奇函数.则函数y=sin(ωx+φ)的一条对称轴为( ).
A.x=(π/2)
B.x=(π/4)
C.x=-(π/8)
D.x=(5π/8)
讲解:从题目的条件可以发现这样两个信息:第一,此函数的周期为π;第二,平移后函数图象过原点.由前者得ω=2;图象向右平移(π/8)后对应的函数解析式为y=sin[2(x-(π/8))+φ],由其过原点知sin(φ-(π/4))=0,又φ为锐角,∴ φ=(π/4).
至此可得原函数为y=sin(2x+(π/4)).再根据此类函数图象的性质:与平衡位置的交点为对称中心,过顶点作x轴的垂线即为对称轴.经检验当x=(5π/8)时此函数取最小值,故应选D.
例3 (1)若函数y=(1+asinx/2-sinx)的值域为[0,2],则a的值为_____.
(2)设直线xcosθ+ysinθ-1=0?(0<θ<(π/2)).①求此直线的倾角φ;②求f(φ)=(sin22φ/cos3φ-cosφ)+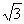 sinφ的值域. sinφ的值域.
讲解:(1)对于此类结构式,一定是用sinx的范围来确定y的范围,途径有两条:一是化部分分式,将变元集中于分母(请独立思考);二是将sinx分离出来,用sinx来反控y的范围:
sinx=(2y-1)/(a+y),∴ |(2y-1)/(a+y)|≤1,平方并化简,得3y2-2(a+2)y+1-a2≤0.由条件知此不等式的解为[0,2],由韦达定理得a=1.
(2)①由题意知tgφ=-(cosθ/sinθ)=-ctgθ=tg((π/2)+θ),∵ 0<θ<(π/2),∴ φ=(π/2)+θ.
②∵ f(φ)=(sin22φ/cos3φ-cosφ)+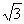 sinφ sinφ
=(sin22φ/-2sin2φsinφ)+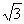 sinφ sinφ
=(-sin2φ/2sinφ)+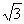 sinφ= sinφ=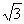 sinφ-cosφ sinφ-cosφ
=2sin(φ-(π/6))=2sin(θ+(π/3)),
而θ+(π/3)∈((π/3),(5π/6)),∴ f(φ)∈(1,2].
例4 在△ABC中,A、B、C为其三个内角,设y=2+cosCcos(A-B)-cos2C.
(1)若任意交换A、B、C的位置,y的值是否发生变化?证明之;
(2)求y的最大值.
讲解:(1)y的值是否变化取决于其表达式是否为轮换对称式,为此注意到为使A、B对称,可将cosC换为-cos(A+B):y=2-cos(A+B)cos(A-B)-cos2C=2-(1/2)(cos2A+cos2B)-(1+cos2C/2)=(3/2)-(1/2)(cos2A+cos2B+cos2C),故y的值不发生变化.
(2)由于变量较多,故应考虑减少变元.方法之一是研究这些变量之间的内在关系,之二是选取主元.对前者,由于三角形的任意性,不易达到目的,对后者较明显的是以C为主元.这时又有两种思维角度:
若运用函数思想,将y视为cosC的二次函数,用配方法y=-[cosC-(cos(A-B)/2)]2+2+(cos2(A-B)/4).当-[cosC-(cos(A-B)/2)]2=0且cos2(A-B)=1同时成立时y取得最大值.这时有A=B且C=(π/3),即△ABC为正三角形时y取最大值(9/4).
若运用方程思想,将原式变形为cos2C-cos(A-B)cosC+y-2=0,视此式为关于cosC的一元二次方程,则Δ=cos2(A-B)-4y+8≥0,即y≤2+(cos2(A-B)/4)≤(9/4),取等号的条件与上面相同.
从本题可以看出,要善于运用数学的观点、思想、方法分析和思考问题,这是提高解题能力的有效途径.
三、专题训练
1.函数y=9-8cosx-2sin2x的最大值是( ).
A.17
B.-1
C.1
D.3
2.若f(x)·sinx是周期为π的奇函数,则f(x)可以是( ).
A.sinx
B.cosx
C.sin2x
D.cos2x
3.若sinα>tgα>ctgα(-(π/2)<α<(π/2)),则α∈( ).
A.(-(π/2),-(π/4))
B.(-(π/4),0)
C.(0,(π/4))
D.((π/4),(π/2))
4.设y=f(x)的定义域为[-1,1],其反函数y=f-1(x)的图象如图3-4.对于f(x)解析式的判定有如下四种:
①f(x)=arcsinx;
②f(x)=arcsinx+(π/2);
③f(x)=arccos(-x);
④f(x)=π-arccosx.
其中错误判定的个数是( ). | 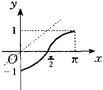
| | 图3-4 | A.0
B.1
C.2
D.3
5.把函数y=2sin((1/2)x+(π/6))的图象向y轴均匀压缩,使图象上所有点的横坐标缩短到原来的(1/3).则图象所对应函数的最小正周期变为________.
6.当x∈(π,(3/2)π)时,arcsin(sinx)=________.
7.已知点P(sinx,cosx),角θ以OP为终边,且为第二象限角,那么函数y=tgx+tgθ的值域是________.
8.设α为锐角,试比较sin2α与sin(α+(π/4))的大小.
9.已知θ∈(0,2π),且sinθcos2θ>0,求θ的取值范围.
10.设0≤θ≤(π/2),f(θ)=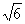 cosθ+ cosθ+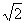 sinθ,g(θ)= sinθ,g(θ)=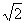 cosθ- cosθ-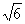 sinθ. sinθ.
(1)当θ为何值时,f(θ)有最大值?
(2)若g(θ)=-(8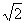 /5),求f(θ)、sinθ的值. /5),求f(θ)、sinθ的值. | 


