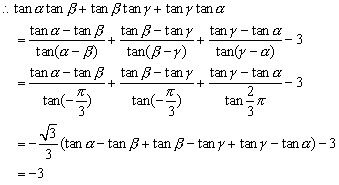两角和的正、余弦
一、选择题
1、已知cos(α＋β)·cos(α－β)=
，则cos2α－sin2β=（
）
A．－
B．－
C． D．
2、已知sinα－sinβ=，cosα－cosβ=
，则cos(α－β)=（ ）
A．
B．
C．
D．－
3、如果
，则
=（
）
A．－
B．
C．
D．－
4、已知3cos(2α＋β)＋5cosβ=0，则log2[tan(α＋β)tanα]2的值是（ ）
A．2 B．4 C．6 D．8
5、如果0<α<
，0<β<，且
，则α＋β=（ ）
A． B．
C．
D．
6、α，β，α＋β均为锐角，A=sinα＋sinβ，B=cosα＋cosβ，C=sin(α＋β)，则它们的大小关系是（ ）
A．C<A<B B．A<B<C C．A>B>C D．B>C>A
7、若sinα，sinβ是方程
的两根，且sinα<sinβ，则锐角α、β的度数分别为（ ）
A．25°，65° B．65°，25° C．15°，75° D．75°，15°
8、α、β、γ都是锐角，
，则α＋β＋γ=（ ）
A． B．
C． D．
9、在△ABC中，
，那么cosC的值是（ ）
A．
B．
C．
D．
10、已知cosβ=a，sinα=4sin(α＋β)，则tan(α＋β)的值是（ ）
A．
B．－ C．±
D．±
窗体底端
二、填空题
11、设tanθ与
是方程x2＋px＋q=0的两个根，则p，q的关系是___________.
12、已知
，则cosx＋cosy的取值范围是___________.
三、解答题
13、已知
，且0<α<<β<π，求cos(β－α)的值.
14、已知cosαcosβ=sinαsinβ，求证：sin(α＋2β)=sinα.
15、设α，β，γ是公差为的等差数列，试求tanαtanβ＋tanβtanγ＋tanγ·tanα的值.
答案：一、CAABB AABCD
1、直接根据结论cos(α＋β)·cos(α－β)=cos2α－sin2β. 2、把两已知条件平方相加.
3、
4、由已知3cos[(α＋β)＋α]＋5cos[(α＋β)－α]=0，可得 8cos(α＋β)cosα＋2sin(α＋β)sinα=0.
即tan(α＋β)tanα=－4.
5、
.
又α＋β∈（0，π），故
.
6、取特值α=β=30°，则A=1，B=
.
7、直接根据求根公式.
8、
又tanr<tanβ<tanα<
，且α、β、γ都是锐角. 故0<α，β，γ<30°，即0<α＋β＋γ<90°.
从而α＋β＋γ =45°.
9、若A为钝角，则由
，知150°<A<180°， 由cosB=
知B>60°，此时A＋B>180°与两角和定理相矛盾. 故A只能是锐角，从而由
可得
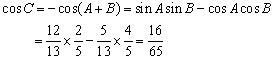
10、由sin[(α＋β)－β]=4sin(α＋β)得 sin(α＋β)cosβ－cos(α＋β)sinβ=4sin(α＋β)
即(cosβ－4)sin(α＋β)=cos(α＋β)sinβ ∴
.
二、11、p－q＋1=0
提示：∵
. ∴
，即1－q=－p
即p－q＋1=0.
12、
提示： 令t=cosx＋cosy，则t2=cos2x＋2cosxcosy＋cos2y， 又
两式相加得
. 由－1≤cos(x－y)≤1，可求出t的范围.
三、13、解：依题意知，
， 故
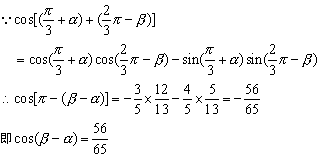
14、证明：
由已知 cosαcosβ－sinαsinβ=0，即cos(α＋β)=0. ∴ sin(α＋2β)=sin[(α＋β)＋β]
=sin(α＋β)cosβ＋cos(α＋β)sinβ=sin(α＋β)cosβ.
又cosβ=cos[(α＋β)－α] =cos(α＋β)cosα＋sin(α＋β)sinα =sin(α＋β)sinα
∴ sin(α＋2β)=sin2(α＋β)sinα ∵ cos(α＋β)=0，即sin2(α＋β)=1. ∴ sin(α＋2β)=sinα.
15、解：由 tan(α－β)=
.
