第五章 平面向量
第一教时
教材：向量
目的：要求学生掌握向量的意义、表示方法以及有关概念，并能作一个向量与已知向量相等，根据图形判定向量是否平行、共线、相等。
过程：
一、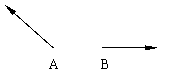
开场白：课本P93（略）
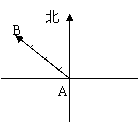
实例：老鼠由A向西北逃窜，猫在B处向东追去，
问：猫能否追到老鼠？（画图）
结论：猫的速度再快也没用，因为方向错了。
二、 提出课题：平面向量
1．意义：既有大小又有方向的量叫向量。例：力、速度、加速度、冲量等
注意：1°数量与向量的区别：
数量只有大小，是一个代数量，可以进行代数运算、比较大小；
向量有方向，大小，双重性，不能比较大小。
2°从19世纪末到20世纪初，向量就成为一套优良通性的数学体系，用以研究空间性质。
2． 向量的表示方法：
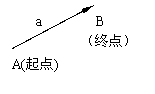
1°几何表示法：点—射线
有向线段——具有一定方向的线段
有向线段的三要素：起点、方向、长度
记作（注意起讫）
2°字母表示法：
可表示为
（印刷时用黑体字）
P95 例 用1cm表示5n mail（海里）
3．
模的概念：向量的大小——长度称为向量的模。
记作： 模是可以比较大小的
4． 两个特殊的向量：
1°零向量——长度（模）为0的向量，记作
。的方向是任意的。
注意与0的区别
2°单位向量——长度（模）为1个单位长度的向量叫做单位向量。
例：温度有零上零下之分，“温度”是否向量？
答：不是。因为零上零下也只是大小之分。
例：与
是否同一向量？
答：不是同一向量。
例：有几个单位向量？单位向量的大小是否相等？单位向量是否都相等？
答：有无数个单位向量，单位向量大小相等，单位向量不一定相等。
三、 向量间的关系：
1．平行向量：方向相同或相反的非零向量叫做平行向量。
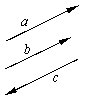记作：∥
∥
规定：与任一向量平行
2． 相等向量：长度相等且方向相同的向量叫做相等向量。
记作：=
规定：=
任两相等的非零向量都可用一有向线段表示，与起点无关。
3． 共线向量：任一组平行向量都可移到同一条直线上 ，
所以平行向量也叫共线向量。
= 
=
=
例：（P95）略
变式一：与向量长度相等的向量有多少个？（11个）
变式二：是否存在与向量长度相等、方向相反的向量？（存在）
变式三：与向量共线的向量有哪些？（
）
四、 小结：
五、 作业：P96 练习 习题5.1