第十二教时
教材：平面向量的数量积的运算律
目的：要求学生掌握平面向量数量积的运算律，明确向量垂直的充要条件。
过程：
一、复习：
1．平面向量数量积（内积）的定义及其几何意义、性质
2．判断下列各题正确与否：
1°若a = 0，则对任一向量b，有a×b = 0。 ( √ )
2°若a ¹ 0，则对任一非零向量b，有a×b ¹ 0。 ( × )
3°若a ¹ 0，a×b = 0，则b = 0。 ( × )
4°若a×b = 0，则a 、b至少有一个为零。 ( × )
5°若a ¹ 0，a×b = a×c，则b = c。 ( × )
6°若a×b = a×c，则b = c当且仅当a ¹ 0时成立。 ( × )
7°对任意向量a、b、c，有(a×b)×c ¹ a×(b×c)。 ( × )
8°对任意向量a，有a2 = a2。 ( √ )
二、 平面向量的运算律
1．交换律：a × b = b × a
证：设a，b夹角为q，则a × b = abcosq，b × a = bacosq
∴a × b = b × a
2．(
a)×b =(a×b) = a×(b)
证：若> 0，(a)×b =abcosq，
(a×b) =abcosq，
a×(b) =abcosq，
若< 0，(a)×b =abcos(p-q) = -ab(-cosq) =abcosq，
(a×b) =abcosq，
a×(b) =abcos(p-q) = -ab(-cosq) =abcosq。
3．(a + b)×c = a×c + b×c
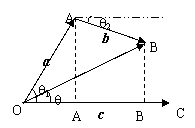在平面内取一点O，作
= a, 
= b，
= c，
∵a + b （即
）在c方向上的投影
等于a、b在c方向上的投影和，
即：a + b cosq = a cosq1 + b cosq2
∴ c a + b cosq =c a cosq1 + c b cosq2
∴c×(a + b) = c×a + c×b 即：(a + b)×c = a×c + b×c
4．例题：P118—119 例二、例三、例四 （从略）
三、应用例题：（《教学与测试》第27课P156 例二、例三）
例一、已知a、b都是非零向量，且a + 3b与7a - 5b垂直，
a - 4b与7a - 2b垂直，求a与b的夹角。
解：由(a + 3b)(7a - 5b) = 0 Þ 7a2 + 16a×b -15b2 = 0 ①
(a - 4b)(7a - 2b) = 0 Þ 7a2 - 30a×b + 8b2 = 0 ②
两式相减：2a×b = b2
代入①或②得：a2 = b2
设a、b的夹角为q，则cosq =
∴q = 60°
例二、求证：平行四边形两条对角线平方和等于四条边的平方和。
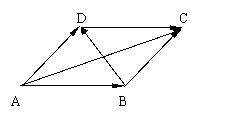
解：如图： ABCD中：
，
，
=
∴2=
而
=
∴2=
∴2 + 2 = 2
= 
四、小结：运算律
五、作业： P119 习题5.6 7、8
《教学与测试》P152 练习