平面向量的数量积平移的综合练习课

第十五教时

教材：平面向量的数量积平移的综合练习课

目的：使学生对平面向量数量积的意义、运算有更深的理解，并能较熟练地处理有关长度、角度、垂直的问题。

过程：

一、复习：

1．平面向量数量积的定义、运算、运算律

2．平面向量数量积的坐标表示，有关长度、角度、垂直的处理方法

3．平移的有关概念、公式

二、  例题

例一、a、b均为非零向量，则 a+b = a-b 是 的………………（C）

　　　A．充分不必要条件　　　　　 B．必要不充分条件　

　　　C．充要条件　　　　　　 　　D．既不充分也不必要条件

　　　解：若a+b = a-b Û a+b² = a-b² Û a² + 2a×b + b² = a² - 2a×b + b²

　　　　　   Û a×b = 0 Û a^b

例二、向量a与b夹角为，a = 2，b = 1，求a+b×a-b的值。

　解：a+b² = a² + 2a×b + b² = 4 + 2×2×1×cos + 1 = 7

　　　∴a+b =,　同理：a-b² = 3, a-b =　 ∴a+b×a-b =

例三、　　  ABCD中，= a，= b，= c，= d，

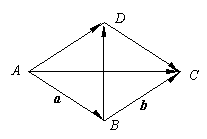
　　　且a×b = b×c = c×d = d×a，问ABCD是怎样的四边形？

　解：由题设：a×bcosB = b×ccosC = c×dcosD = d×acosA

　　　∵a = c , b = d　 ∴cosA = cosB = cosC = cosD = 0

　　　∴　ABCD是矩形

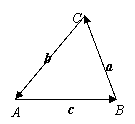
例四、  如图△ABC中，= c，= a，= b，

　　　 则下列推导不正确的是……………（D）

　　　A．若a ×b < 0，则△ABC为钝角三角形。

　　　B．若a ×b = 0，则△ABC为直角三角形。

　　　C．若a ×b = b×c，则△ABC为等腰三角形。

D．若c×(a + b + c) = 0，则△ABC为正三角形。

　　　　解：A．a×b = abcosq < 0，则cosq < 0，q为钝角

　　　　　  B．显然成立

　　　　　  C．由题设：acosC = ccosA，即a、c在b上的投影相等

　　　　　  D．∵a + b + c = 0, ∴上式必为0，∴不能说明△ABC为正三角形

例五、　已知：a =，b = 3，a与b夹角为45°，求使a+b与a+b夹角为锐角的的取值范围。

　解：由题设：a×b = abcosa = 3××= 3

　　　(a+b)×(a+b) =a² +b² + (² + 1)a×b = 3² + 11 + 3

　　　∵夹角为锐角　 ∴必得3² + 11 + 3 > 0

　　　∴ 或

例六、i、j是平面直角坐标系内x轴、y轴正方向上的两个单位向量，

　　　且= 4i + 2j，=3i + 4j，

　　　证明：△ABC是直角三角形，并求它的面积。

　解：= (4, 2), = (3, 4), 则= (3-4, 4-2) = (-1, 2), = (-4, -2),

　　　∴×= (-1)×(-4) + (-2)×2 = 0　 ∴^

　　　即△ABC是直角三角形

　　　 =,　 =,　且ÐB = 90°,

　　　∴S_△ABC =

例七、用向量方法证明：菱形对角线互相垂直。

　证：设== a , == b

　　　∵ABCD为菱形　　 ∴a = b

　　　∴×= (b + a)(b - a) = b² - a² = b² - a² = 0

　　　∴^

例八、已知a、b都是非零向量，且a + 3b与7a - 5b垂直，

　　　a - 4b与7a - 2b垂直，求a与b的夹角。

　　　解：由(a + 3b)(7a - 5b) = 0 Þ 7a² + 16a×b -15b² = 0　　①

　　　　　  (a - 4b)(7a - 2b) = 0 Þ 7a² - 30a×b + 8b² = 0　　②

　　　　  两式相减：2a×b = b²

　　　　  代入①或②得：a² = b²

　　　　  设a、b的夹角为q，则cosq =　 ∴q = 60°

三、  作业： P150　复习参考五　A组　19—26

　　　　　　　　　　　　　　 B组　1—6