高一下数学月考练习一
1.若![]() 则θ所在象限是A第一B第二C第三D第四
则θ所在象限是A第一B第二C第三D第四
2.若![]() 则
则![]() (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.下列各式中正确的是A. cos(kπ-α)=-cosα,k∈Z B. sin(kπ-α)=(-1)ksinα, k∈Z
C. cos((α-kπ)= (-1)k+1cosα, k∈Z D. tg(α-kπ)=tgα, k∈Z
4.角![]() 的终边过点
的终边过点![]() ,则
,则![]() 的值等于A.
的值等于A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5.若sin(α![]() ,则cos(
,则cos(![]() +α)=A.
+α)=A.
![]() B
.-
B
.-![]() C .
C . ![]() D. -
D. -![]()
6.集合![]() ,则M∩N中元素的个数是
,则M∩N中元素的个数是
(A)5个 (B)7个 (C)9个 (D)3个
7.如果f(sinx)=cos![]() x,,那么f(cosx)等于A.-sin
x,,那么f(cosx)等于A.-sin ![]() x B. -cos
x B. -cos![]() x
C. sin
x
C. sin![]() x D. cos
x D. cos![]() x
x
8.函数![]() 的值是 ( )
的值是 ( )
(A){0,-1} (B){0,1} (C){0,![]() } (D){0,-1,1}
} (D){0,-1,1}
9.有常数![]() 使得等式
使得等式![]() 和
和![]() 同时成立,则
同时成立,则![]() 的一个值是( )
的一个值是( )
A. ![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
10.设![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,
项和,![]() ,若
,若![]()
![]() ,且
,且![]() ,那么
,那么![]() 的值为: A. 30 B. 31 C. 28 D. 29
的值为: A. 30 B. 31 C. 28 D. 29
11.已知等比数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() 等于A. 64 B. 66 C.
等于A. 64 B. 66 C. ![]() D.
D. ![]()
12.设![]() 的前
的前![]() 项和
项和![]() ,则
,则![]() 是数列为等比数列的( )条件。
是数列为等比数列的( )条件。
A.充分不必要 B.必要非充分 C.充要 D.即不充分也不必要
13.数列![]() 中,
中,![]() ,
,![]() ,又数列
,又数列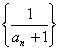 为等差数列,则
为等差数列,则![]() =
=
14.函数![]() 的最小值是_______________.
的最小值是_______________.
15.已知![]()
16.设![]() ,则
,则![]() =
.
=
.
17.已知![]() 则α=
;
则α=
;
β= .
18.若函数y=x2+(a+2)x+3,x∈[a,b]的图象关于直线x=1对称,则b= .
19.设f(x)=,利用课本中推导等差数列前n项和的公式的方法,可求得f(-5)+f(-4)+……+f(0)+……+f(5)+f(6)的值为 .
20.已知集合A={xx≤2,x∈R},B={xx≥a}且AÍB,则实数a的取值范围是 .
21. (10分) 解不等式组
22.(12分)已知α终边上有一点P(3,y),且cosα=![]() ,求
,求![]() 及
及![]() ,
,![]() 的值.
的值.
23. (12分)某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护需50元.(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
24. (12分)已知函数![]() (1) 证明f(x)是奇函数;并求f(x)的单调区间(2) 分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,由此概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式,并加以证明.
(1) 证明f(x)是奇函数;并求f(x)的单调区间(2) 分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,由此概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式,并加以证明.
25. (12分)在一次人才招聘会上,有A、B两家公司分别开出了它们的工资标准:A公司允诺第一个月工资为1500元,以后每年月工资比上一年月工资增加230元;B公司允诺第一年月工资数为2000元,以后每年月工资在上一年的月工资基础上递增5%,设某人年初被A、B两家公司同时录取.试问: (1) 若该人分别在A公司或B公司连续工作n年,则他在第n年的月工资收入分别是多少?
(2) 该人打算连续在一家公司工作10年,仅从工资收入总量较多作为应聘的标准(不记其它因素),该人应该选择哪家公司,为什么?
附加题:已知函数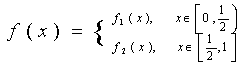
 其中
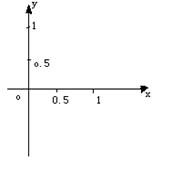
其中![]() (Ⅰ)在下边坐标系上画出y=f(x)的图象(Ⅱ)设y=
(Ⅰ)在下边坐标系上画出y=f(x)的图象(Ⅱ)设y=![]()
![]()
![]()
![]()
![]() 求数列
求数列![]() 的通项公式;
的通项公式;
(Ⅲ)若![]()
1C 2C 3B 4D 5C 6B 7C 8D 9D 10A 11C 12C
13 1/2 14.2 15K=-1 л 3л/2 16.-1 17±л/4, л/3 2л/3
18, 6 19,3 20, (-∞,-2)
21原不等式组ó
ó 1<x<2 或4<x<5
.
∴ 解集为{x1<x<2 或4<x<5= .
22解:![]() ∴y=±9
∴y=±9
当y=9时,![]()
![]()
当y=-9时,![]()
![]()
23解:(Ⅰ)当每辆车的月租金定为3600元时,未租出的车辆数为![]() ,所以这时租出了88辆车.
,所以这时租出了88辆车.
(Ⅱ)设每辆车的月租金定为x元,则租赁公司的收益为
![]() ,
,
整理得![]()
![]() .
.
所以,当x=4050时,f(x)最大,最大值为f(4050)=307050,
即当每辆车的月租金定为4050时,租赁公司的月收益最大,
最大月收益为307050元.
24证明: ∵ f(x)的定义域为D={xx∈R,x≠0}
设x是D内任意一个值,
则f(-x)=![]() =-f(x)
=-f(x)
∴ f(x)为奇函数
由题意可得f'(x)=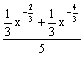 ,显然f'(x)>0恒成立
,显然f'(x)>0恒成立
又当x2= 时,f(x2)= <0,当x1=
- 时,f(x1)= >0
即当x1<x2时,有f(x1)>f(x2),加上条件f'(x)>0,不能说明f(x)在定义域D内不是增函数。
但是在x∈(-∞,0)时,有f'(x)>0
在x∈(0,+∞)时,有f'(x)>0
∴ f(x)的单调递增区间是(-∞,0)和(0,+∞)
(2)计算f(4)-5f(2)g(2)
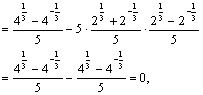
同理可计算得f(9)-5f(3)g(3)的值等于0,
由此概括出,涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式为:f(x2)-5f(x)g(x)=0
其证明如下:
f(x2)-5f(x)g(x)
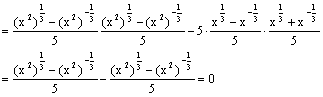
故f(x2)-5f(x)g(x)=0得证。
25(1)在A公司连续工作n年,则第n年的月工资为
an=1500+230(n-1)=230n+1270(元)
在B公司连续工作n年,则第n年的月工资为
bn=2000(1+)n-1=2000×1.05n-1(元)
(2)在A公司连续工作10年,则其工资总收入为
S10=[12×(1500+1500+9×230)×10]=304200(元)
在B公司连续工作10年,则其工资总收入为
S'10==30420(元)
S10>S'10,故仅从工资收入总量来看,该人应该选择A公司。