高一下学期 数学 每周一练试题
班级 座号 姓名 评分
一、 选择题：（30分）
1．对于第四象限角的集合，下列四种表示中错误的是 （ ）
A. {θ k·360º+270º<θ<k·360º+360º，k∈Z}； B. {θ k·360º-90º<θ<k·360º，k∈Z};
C. {θ k·360º+270º<θ<k·360º，k∈Z}； D. {θ k·360º+630º<θ<k·360º+720º，k∈Z}.
2．角α= k·180º+45º，k∈Z的终边落在 （ ）
- 第一或第四象限； B. 第一或第二象限； C. 第二或第四象限； D. 第三或第四象限.
3．设P={锐角}，Q={小于90º的角}，R={第一象限的角}，S={小于90º的正角}，则下列六个关系中：①
P=Q； ②
P=R；③
P=S；④
P
Q；⑤
PR；⑥
QR正确的有
（ ）
A. 1个； B. 2个； C. 3个； D. 4个.
4．下列各对角中，终边相同的是 （ ）
A. 
和
（k∈Z）； B. 
和
；
C. 
和
；
D. 
和
.
5．若α、β的终边关于原点对称，则 （ ）
A. α=β； B. α= -β； C. α=β±π； D. α=(2k+1)π+β，（k∈Z）.
6．已知集合A={α 2kπ≤α≤(2k+1)π，（k∈Z）}，B={α -4≤α≤4}，则A∩B等于
（ ）
A. Ф； B. {α -4≤α≤4}； C. {α 0≤α≤π}； D. {α-4≤α≤-π或0≤α≤π}.
二、 填空题：（15分）
7．集合A={ββ=k·360º+60º，k∈Z}；B={ββ=k·720º+60º，k∈Z}；
C={ββ=k·180º+60º，k∈Z}，那么集合A、B、C的关系是 。
8．θ为小于360º的正角，这个角的7倍角的终边与这个角的终边重合，则θ= 。
9．在半径为1的圆中，圆心角为周角的
的角所对的弧长是
；含这段弧的扇形的面积是
；含这段弧的弓形的面积是
。
三、 解答题：（55分）
10．写出与-1840º终边相同的角的集合S ；若α∈S，且α∈[-720º，360º]，求α.
11．写出终边在各图中阴影部分的角的集合（虚线表示不含边界，实线表示含边界）。
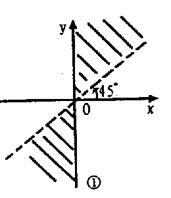
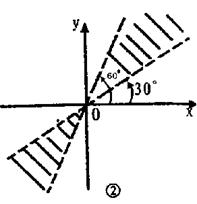
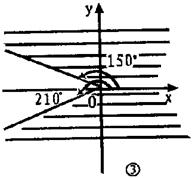
12．试判断弧度数分别是6、7、65、66的角所在的象限。
13．时针指到3点后，当时针又经过1小时55分钟时，时针至分针的夹角是多少度？合多少弧度？