基础测试
（一）选择题（每小题4分，共24分）
1．下列各函数中，图象完全相同的是（ ）．
（A）y＝2 lg x和y＝lg x2
（B）y＝
和 y＝x
（C）y＝
和y＝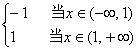
（D）y＝x－3和y＝
【答案】（C）．
【点评】应考察每组两个函数的定义域和对应法则是否相同．
2．设f（x）＝
（x∈R且x≠－
），则f －1 （2）等于（ ）．
（A）－
（B）
（C）
（D）－
【答案】（A）．
【点评】运用反函数的概念，只需在原函数中令2＝，解出x，即为所求．
3．设a＝0.32，b＝log20.3，c＝20.3，这三个函数之间的大小关系是（ ）．
（A）a ＜c ＜b （B）a ＜b ＜c
（C）b ＜a ＜c （D）b ＜c ＜a
【答案】（C）．
【点评】三个数中a ＞0，c ＞0，b ＜0，否定（A），（B）．而a ＜1，c＞1，故选（C）．
4．若loga2 ＜logb2 ＜0，则（ ）．
（A）0＜a ＜b ＜1 （B）0＜b ＜a ＜1
（C）a ＞b ＞1 （D）b ＞a ＞1
【答案】（B）．
【点评】利用对数函数的图象和性质以及换底公式可解．
【提示】loga 2＝
，logb 2＝
，
由 ＜＜0，
得 0＞log2 a ＞log2 b，
∴ 1＞a ＞b ＞0．
5．将函数y＝f（x－1）的图象作适当的平移，可得到函数y＝f（x＋2）的图象，这个平移是（ ）．
（A）向左平移3个单位 （B）向右平移3个单位
（C）向左平移2个单位 （D）向右平移2个单位
【答案】（A）．
【点评】函数y＝f（x＋a）（a ＞0）的图象是由y＝f（x）向左平移a个单位得到的．将y＝f（x－1）的图象向左平移3个单位，就得到y＝f（x＋3－1）＝f（x＋2）的图象．
6．函数f（x）＝
在区间（－2，＋∞）上是增函数，那么a 的取值范围是（ ）．
（A）0＜a ＜
（B）a ＞
（C）a ＜－1或a ＞1 （D）a ＞－2
【答案】（B）．
【点评】利用反比例函数的单调性，函数y＝a＋
即（x＋2）（y －a）＝1－2 a ．若在（－2，＋∞）上是增函数，只需1－2 a ＜0，故a ＞．
（二）填空题（每小题5分，共25分）
1．若（x，y）在一一映射下的象是（x＋y，x－y），其中x∈R，y ∈R，则（1，2）的象是_________；（1，－3）的原象是___________．
【答案】（3，－1）；（－1，2）．
2．已知函数y＝2 x2＋4 （a －4） x＋5，在（－∞，－3）上是减函数，则a 的取值范围是________．
【答案】a ≤7．
【点评】要切实掌握好二次函数的定义及有关的性质，本题中函数图象对称轴方程是x＝4－a，且开口向上，故只要4－a ≥－3即可．
3．函数f（x）＝log2（3－2 x－x2）的值域是___________．
【答案】（－∞，2
．
【点评】复合函数的值域问题，要注意先求函数的定义域，从而求出u＝3－2 x－x2＞0的值域，再利用对数函数y＝log2 u性质求得答案．
4．函数y＝log0.5（x2＋x－6）的单调区间是___________．
【答案】增区间为（－∞，－3），减区间为（2，＋∞）．
【点评】复合函数的单调性问题，要注意增增“增”、减增“减”、增减“减”、减减“增”等规律．y＝log0.5 u是减函数，因此只要求出u＝x2＋x－6的单调区间即可，本题容易忽视函数的定义域而导致错误．
5．已知函数f（x）是R 上的奇函数，且当x∈（0，＋∞）时，f（x）＝x（1＋
），那么当x∈（－∞，0）时，f（x）＝__________．
【答案】本题中的f（x）是一个分段函数，要能够正确运用奇函数的性质，利用x＞0时函数的解析式，得出x＜0时的解析式．要注意求谁的解析式以谁为主，设x＜0，则
－x＞0，
∴ f（－x）＝－x（1＋
）＝－x（1－），而f（－x）＝－f（x）．
∴ f（x）＝x（1－）．
（三）解答题（本题共4小题，共51分）
1．（本小题共12分）
等腰梯形ABCD 下底AB＝10，上底DC＝4，两腰AD＝BC＝5，动点P 由B 点沿折线BCDA 向A 运动，设P 点移动的距离为x，△ABP 的面积为y，求函数y＝f（x）．
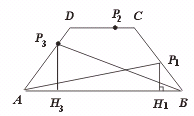
【略解】如图，可知等腰梯形的高为4，当P 点运动到P1位置时，△AP1B的高P1H1＝
．
∴ 此时
＝×10×，
当P 点运动到P3位置时，△AP3B的高P3H3满足：
＝
，
此时
＝×10×
，
当P点在CD上时，＝h×AB＝×4×10＝20
∴ y＝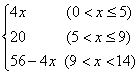
【点评】画图，利用图形思考，是一项基本功．本题运用的分类讨论思想，数形结合思想是中学数学中重要的思想方法．
2．（本题共13分）
设0≤x≤1，x为变量，a 为常数，求函数f（x）＝ （4－3 a） x2－2 x＋a 的最大值．
【略解】若4－3 a＝0，则f（x）＝－2 x＋
是单调减函数，
∴ f（x）最大值为f（0）＝a＝；
若4－3 a ≠0，则f（x）为二次函数，其对称轴方程为：
x＝
，
f（0）＝a，f（1）＝2－2 a．
当a ＞
时，f（0）＞f（1）；
当a ＜时，f（0）＜ f（1）；
∴ f（x）的最大值为f（1）＝2－2 a ；
当a 取其他实数时，f（x）的最大值为f（0）＝a ．
【点评】二次函数是中学数学中的重要函数之一．二次函数的有关性质，特别是在闭区间上求二次函数的最值问题应该熟练掌握．本题中的二次函数含有参数a，应注意分类讨论思想的应用．
3．（本题共13分）
已知函数f（x）＝lg（ax2＋2 x＋1），
（1）若函数f（x）的定义域为R，求实数a的取值范围；
（2）若函数f（x）的值域为R，求实数a的取值范围．
【略解】（1）ax2＋2 x＋1＞0恒成立，只需D＝4－4 a ＜0，且a ＞0，即a ＞1，满足题意．
（2）若f（x）的值域为R，则需u＝ax2＋2 x＋1能取遍一切正数，需满足a ＞0且
D＝4－4 a ≥0，即0＜a ≤1为所求．
【点评】
许多同学做此题时，不能理解（2）题的题意，关键是欲使f（x）的值域为R，则必需u＝ax2＋2 x＋1能取遍一切正数，所以抛物线的开口向上，且与x轴要有交点．
4．（本题共13分）
已知函数f（x）＝lg（a x－b x）（a ＞1＞b ＞0）
（1）求f（x）的定义域；
（2）判断f（x）的单调性，并予以证明；
（3）当a，b 满足什么关系时，f（x）在（1，＋∞）内取正值，而不在（1，＋∞）上则不取正值．
【略解】（1）a x－b x＞0 
（
） x＞1，而＞1，
∴ f（x）的定义域为：x＞0，
（2）利用函数单调的定义证明f（x）在（0，＋∞）上是增函数，（略）
（3）利用（2）的解法及所给条件应有f（1）＝0．即由lg（a －b）＝0，故a －b＝1为所求．