提高测试(二)
(本试卷共10个题,每题10分)
1.求函数y=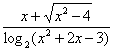 的定义域.
的定义域.
【略解】x的取值范围,应满足
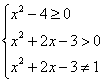
![]() x<-3且x≠-1-
x<-3且x≠-1-![]() .
.
【点评】
函数的定义域是函数的基本性质之一,应掌握求函数定义域的方法,实际上就是解x所满足的不等式组.
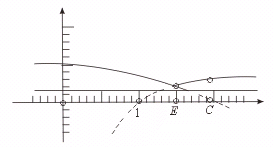
2.当k ∈(0,![]() )时,函数y=
)时,函数y=![]() 的图象与函数y=kx的图象有多少个不同的交点?
的图象与函数y=kx的图象有多少个不同的交点?
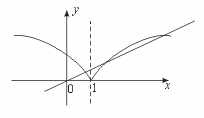
【略解】先作出函数y=![]() 的图象.
的图象.
.
函数y=kx,k ∈(0,![]() )的图象是一条直线,两个函数的图象只可能在第一象限内相交.
)的图象是一条直线,两个函数的图象只可能在第一象限内相交.
当直线y=kx,k ∈(0,![]() )与函数y=
)与函数y=![]() 在x>1上的部分相切时,方程
在x>1上的部分相切时,方程
![]() =kx应有重根,即二次方程的判别式为0,D=1-4 k2=0,得k=
=kx应有重根,即二次方程的判别式为0,D=1-4 k2=0,得k=![]() .
.
所以,当0<k <![]() 时,两个图象在x>1时相交于两个点.
时,两个图象在x>1时相交于两个点.
故两个函数的图象有3个交点.
【点评】本题充分体现了数形结合的数学思想方法.在利用图象解题时,要注意用代数的方法解决相交和相切时的数量关系.
3.解方程
(![]() ) x+(
) x+(![]() ) x=10.
) x=10.
【略解】 ∵ ![]() =1,
=1,
∴ 原方程可以改写为:(![]() ) x+(
) x+(![]() ) x=10,
) x=10,
设y= (![]() ) x,则y+
) x,则y+![]() =10,解得y=5±2
=10,解得y=5±2![]() ,
,
于是由(![]() ) x=5±2
) x=5±2![]() ,得x=±2,
,得x=±2,
∴ 原方程的解为:x=±2.
【点评】
![]() 本题的关键是注意到
本题的关键是注意到![]() 和
和![]() 互为倒数,利用整体换元的思想使问题易于解决.
互为倒数,利用整体换元的思想使问题易于解决.
4.已知函数f(x)=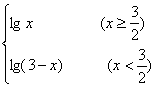 ,若方程f(x)=k 无实根,则实数k 的取值范围是________.
,若方程f(x)=k 无实根,则实数k 的取值范围是________.
【略解】函数f(x)的图象如下图所示,方程f(x)=k 的根,即f(x)的图象与直线g=k 交点的横坐标,由图可见,当k <lg![]() 时,f(x)的图象与直线y=k无交点,即方程f(x)=k 无实根,故k 的取值范围是(-∞,lg
时,f(x)的图象与直线y=k无交点,即方程f(x)=k 无实根,故k 的取值范围是(-∞,lg![]() ).
).
5.对于函数f(x)=loga x(其中a >0,a ≠1),若f(3)-f(2)=1,则
f(3.75)+f(0.9)的值等于_________.
【略解】由f(3)-f(2)=loga3-loga 2=loga![]() =1,∴ a=
=1,∴ a=![]() .
.
∴ f(3.75)+f(0.9)=log a3.75×0.9=log a3.375=loga1.53=3 loga 1.5=3.
6.已知二次函数f(x)=ax2+bx,且f(x1)=f(x2)(x1≠x2),则f(x1+x2)=_____.
【略解】由f(x1)=f(x2),将a(x1+x2)(x1-x2)+b(x1-x2)=0
∵ x1 ≠x2,
∴ a(x1+x2)+b=0.
∴ f(x1+x2)= f(-![]() )=
)=![]() =0.
=0.
7.若函数f (x)=25- x+1 -4×5- x+1 -m 的图象与x轴有交点,则实数m 的取值范围是_____.
【略解】f(x)可看作关于5- x+1 =t 的二次函数(t ≤1)t 2 -4 t-m,为使它的图象与x轴有交点,只须Dt ≥0,而Dt=16+4 m ≥0,故m的取值范围是m ≥-4.
8.设函数f(x)=![]() ,函数g(x)与y=f -1(x+1)的图象关于直线y=x对称,那么g(3)=_______.
,函数g(x)与y=f -1(x+1)的图象关于直线y=x对称,那么g(3)=_______.
【略解】x=f -1 ( y )=![]() ,x=g-1 (y)=f -1 (y+1)=
,x=g-1 (y)=f -1 (y+1)=![]() ,y=g(x)=
,y=g(x)=![]() ,
,
故g(3)=![]() .
.
9.定义在自然数集上的函数f(x),x∈N,f(1)=1,f(m+n)=f(m)+f(n)+m · n,m,n ∈N.求f(x).
【略解】令m=1,代入上式,得f(1+n)=f(1)+f(n)+n=f(n)+(n+1),
即 f(n+1)-f(n)=n+1.
取n=1,2,3,…,x-1,得
f(2)-f(1)=2
f(3)-f(2)=3
……
f(x)-f(x-1)=x+1.
以上各式相加,得f(x)-f(1)=2+3+…+(x+1).
∴ f(x)=![]() (x∈N).
(x∈N).
10.设f(x)=3 x-2 f(![]() ),x≠0.求f(x).
),x≠0.求f(x).
【略解】令y=![]() ,则x=
,则x=![]() ,代入方程,
,代入方程,
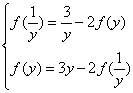 消去
消去![]() ,得f(y)=
,得f(y)=![]() .
.
故 f(x)=![]() .
.