提高测试（一）
（一）选择题（每小题4分，共24分）
1．已知函数f（x）的定义域为[a，b ]且b ＞－a ＞0，则函数F（x）＝f （ x）＋f （－x）的定义域是（ ）．
（A）[a，－a ] （B）（－∞，－a）
[a，＋∞
（C）[－a，a ] （D）（－∞，a）[－a，＋∞
【答案】（A）．
【点评】本题考查函数定义域的概念，F （x） 的定义域应满足a ≤x≤b，且a ≤－x≤b，
即
解答本题应正确在数轴上画出所示区域，借肋图形得到答案．
2．已知函数f（x）＝a x＋b 的图象经过点（1，7）其反函数f －1（x）的图象经过点（4，0），则f（x）的表达式是（ ）．
（A）f（x）＝3 x＋4 （B）f（x）＝4 x＋3
（C）f（x）＝2 x＋5 （D）f（x）＝5 x＋2
【答案】（B）．
【点评】运用f（x）和f －1 （x）的关系，f －1 （x）的图象经过（4，0）点，可知原来的函数f（x）必过点（0，4）．
3．已知f（x）＝2 x＋3，g（x）＝4 x－5，若f [p（x）]＝g（x），则p（3）的值为（ ）．
（A）2 （B）±2 （C）－2 （D）不能确定
【答案】（B）．
【点评】本题考察函数概念的对应法则，由已知：2 p（x）＋3＝4 x－5，所以 p（x）＝2 x－4，∴ p（3）＝2，故 p（3）＝±2．
4．设f（x）＝ax7＋bx3＋cx－5其中a，b，c 为常数，如f（－7）＝7，则f（7）等于（ ）．
（A）－17 （B）－7 （C）14 （C）21
【答案】（A）．
【点评】本题考察函数奇偶性的灵活运用，f（x）是一个非奇非偶函数，注意到：f（x）＝g（x）－5，而g（x）是一个奇函数，由f（－7）＝g（－7）－5＝7，得g（－7）＝－12，故f（7）＝g（7）－5＝－12－5＝－17．
5．已知1＜ x＜d，令a＝（logd x） 2，b＝logd （x2 ），c＝logd （logd x），则（ ）．
（A）c ＜b ＜c （B）a ＜c ＜b
（C）c ＜b ＜a （D）c ＜a ＜b
【答案】（D）．
【点评】比较大小采用的方法之一是“中间值”法，如本题中将a，b，c 先与0比较，知a ＞0，b ＞0，而c ＜0．利用“函数的单调性”或“比较法”等可解．
6．下列命题中，正确的命题是（ ）．
（A）y＝2 lg x与y＝lg x2是同一个函数
（B）已知f（x）是定义在R上的一偶函数，且在[a，b ]上递增，则在[－b，－a ]上也递增
（C）f（x）＝ log2 x是偶函数
（D）f（x）＝loga （
）的奇函数
【答案】（D）．
【提示】（A）中两个函数的定义域不同，前者x＞0，后者x≠0；（B）中，在[－b，－a]上应递减；（C）中f（x）的定义域是x＞0，所以f（x）既不是奇函数也不是偶函数．
（二）填空题（每小题5分，共25分）
1．若函数y＝
，x∈[－2，－1]，则其反函f －1 （x）＝______．
【答案】f －1 （x）＝－
（－
≤x≤－
）．
【点评】要切实掌握好求反函数的一般步骤，还需特别注意，反解x时，x的取值范围，如本题中，由x2＝
＋6，求x时，开方应取“负”．另外，求反函数，必须证明反函数的定义域，可通过求原函数的值域完成．
2．已知函数f（x）的定义域是[－1，2] 则函数f（x2）的定义域是________．
【答案】[－
，]．
【提示】解不等式：－1≤ x2≤2可得．
∴ 0≤ x≤，∴ －≤ x≤．
3．已知f（n）＝
n ∈N，则f（5）的值等于________．
【答案】8．
【点评】考查对对应法则f的理解．f（5）＝f [ f（5＋5）]＝f [ f（10）]＝f（10－3）＝f（7）
＝f [ f（7＋5）]＝f（12－3）＝f [ f（9＋5）]＝f（14－3）＝f（11）＝11－3＝8．
4．函数y＝2 lg（x－2）－lg（x－3）的最小值为_________．
【答案】x＝4时，y min＝lg 4．
5．方程log2（9 x－1＋7）＝2＋log2（3 x－1＋1）的解为________．
【答案】x＝1或x＝2．
由9 x－1＋7＝4（3 x－1＋1），得（3x－1） 2－4 · 3 x－1＋3＝0，故3 x－1＝1或3可解．
（三）解答题（共4个小题，满分51分）
1．（本题满分12分）
设函数y＝f（x）是定义在（－1，1）上的奇函数，且在[0，1上是减函数，若f（t－1）＋f（2 t －1）＞0，求t 的取值范围．
【略解】由已知，f（2 t －1）＞－f（t －1）＝f（1－t）（*），
又f（x）在[0，1）上是减函数且是奇函数，
∴ f（x）在（－1，1）上是减函数，故（*）式等价于：
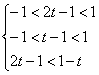
0＜t ＜
为所求．
【点评】本题考查函数的奇偶性和单调性的应用．在由函数值的大小关系，利用单调性得两个自变量值之间的关系时，一定要将两个自变量落在同一个单调区间内．
2．（本题满分13分）
已知f（x）＝loga
（a ＞0，a ≠1）．
（1）求f（x）的定义域；
（2）判断f（x）的单调性，并予以证明；
（3）求使f（x）＞0的x取值范围．
【略解】（1）∵ ＞0，∴ f（x）定义域为（－1，1）．
（2）设－1＜x1＜x2＜1，则
f（x1）－f（x2）＝loga
－loga
＝loga
＝loga
∵ －1＜x1＜x2＜1，∴ x2－x1＞0，
∴ （1－x1x2）＋（x2－x1）＞（1－x1x2）－（x2－x1）
即
＜1．
∴ 当a ＞1 时，f（x1）＜f（x2），在（－1，1）上是增函数．
当0＜a ＜1时，f（x1）＞f（x2），在（－1，1）上是减函数．
（3）当a ＞0时，欲f（x）＞0，则有＞1，解得0＜x＜1．
当0＜a ＜1时，欲f（x）＞0，则有0＜＜1，解得－1＜x＜0．
【点评】本题综合考查了函数的定义域；用定义证明函数的单调性，对数的有关概念及解不等式的问题．
3．（本题满分13分）
已知a ∈N，关于x的方程lg（4－2 x2）＝lg（a－x）＋1有实根，求a及方程的实根．
【略解】 由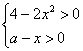
解得－＜x＜且x＜a，
又 方程4－2 x2＝10（a－x），
整理得：x2－5 x＋5 a －2＝0，D＝25－4（5 a －2）≥0，
得a ≤
，
又 a ∈N，∴ a＝1．
此时方程化为：x2－5 x＋3＝0，
∴ x＝
；
又
－＜x＜1，∴ x＝
．
4．（本题满分13分）
已知函数f（x）的定义域为全体实数，且对任意x1，x2∈R有
f （x1）＋f （x2）＝2 f（
）f（
）
成立，又知f（a）＝0（a ≠0，a 为常数），但f（x）不恒等于0，求证：
（1）f（x）是周期函数，并求出它的一个周期；
（2）f（x）是偶函数；
（3）对任意x∈R，有f（2 x）＝2 f 2（x）－1成立．
【略解】（1）令x1＝x＋2 a，x2＝x，由已知可得：
f（x＋2 a）＋f（x）＝2 f（
）f（
）＝2 f（x＋a）·f（a）＝0，
∴ f（x＋2 a）＝－f（x），从而f（x＋4 a）＝－f（x＋2 a）＝f（x）．
∴ 4 a是f（x）的一个周期．
（2）令x1＝x，x2＝－x，
则f（x）＋f（－x）＝2 f（0）f（x）
再令x1＝x2＝x，则
f（x）＋f（x）＝2 f（x）f（0）．
∴ f（x）＋f（－x）＝f（x）＋f（x）．
即 f（－x）＝f（x）．∴ f（x）是偶函数．
（3）由2 f（x）＝2 f（x）f（0）且f（x）≠0，知f（0）＝1．
令x1＝2 x，x2＝0，则有f（2 x）＋f（0）＝2 f（x）f（x），
即 f（2 x）＝2 f 2（x）－1得证．
【点评】若函数f（x）对定义域内任意x满足f（x＋T）＝f（x）（T是一个不为零的常数），则f（x）是以T为周期的函数．有关周期函数的概念在本章教材中还没有涉及到．