第三章《数列》基础测试题1

基础测试

（90分钟，满分100分）

（一）选择题（每小题4分，共40分）

1．已知数列｛a_n｝中，a₁＝a₂＝1，a_n＋2＝a_n＋1＋a_n 对所有自然数n 都成立，则a₁₀＝（　　）．

（A）34　　（B）55　　（C）89　　（D）100

【提示】由a₁，a₂ 算出a₃，再由a₂，a₃ 算出a₄，以此类推算出a₁₀ ．

【答案】（B）．

2．数列1，3，7，15，…的通项公式a_n 等于（　　）．

（A）2ⁿ　　（B）2ⁿ＋1　　（C）2ⁿ－1　　（D）2^n－1

【提示】排除法．由已知，各项均为奇数．所以（A）、（D）不正确．对于（B），由于n＝1时，2¹＋1＝3．所以（B）也不正确．也可以直接归纳出2ⁿ－1．

【答案】（C）．

3．已知等差数列的公差为d，它的前n 项和S_n＝－n²，那么（　　）．

（A）a_n＝2 n－1，d＝－2　　　（B）a_n＝2 n－1，d＝2

（C）a_n＝－2 n＋1，d＝－2　　（D）a_n＝－2 n＋1，d＝2

【提示】由S_n＝－n² 知，a₁＝S₁＝－1，a₂＝S₂－a₁＝－3，从而d＝－2，且a_n＝a₁＋（n－1）d＝－1＋（n－1）·（－2）＝－2 n＋1．

【答案】（C）．

4．某细菌在培养过程中，每20分钟分裂一次（一个分裂为两个），经过3小时，这种细菌由一个可分裂成（　　）．

（A）511　　（B）512　　（C）1023　　（D）1024

【提示】此为a₁＝1，q＝2的等比数列．由于经过第一个20分钟，对应着n＝2，所以经过3小时，对应着n＝10．故所求为a₁₀ ．

【答案】（B）．

5．一架飞机起飞时，第一秒滑跑2.3米，以后每秒比前一秒多滑跑4.6米，离地的前一秒滑跑66.7米，则滑跑的时间一共是（　　）．

（A）15秒　　（B）16秒　　（C）17秒　　（D）18秒

【提示】此为a₁＝2.3，d＝4.6的等差数列，已知a_n＝66.7，求n ．

【答案】（A）．

6．在a 和b（a ≠b）两数之间插入n 个数，使它们与a、b 组成等差数列，则该数列的公差为（　　）．

（A）　　（B）　　（C）　　（D）

【提示】b＝a＋[（n＋2）－1]d ．

【答案】（B）．

7．数列｛a_n｝中，a_n＝－2 n＋100，当前n 项和S_n 达到最大值时，n 等于（　　）．

（A）49　　（B）50　　（C）51　　（D）49或50

【提示】令a_n＝－2 n＋100≥0，得n≤50．即a₄₉ 以前各项均为正数，a₅₀＝0，故S₄₉ 或S₅₀ 最大．

【答案】（D）．

8．等比数列｛a_n｝的首项a₁＝－1，前n 项和为S_n，若＝，则等于（　　）．

（A）－　　（B）－　　（C）　　（D）

【提示】由已知可求得q＝－．

【答案】（A）．

9．已知数列｛a_n｝的通项公式a_n＝，则它的前8项和S₈ 等于（　　）．

（A）　　（B）　　（C）　　（D）

【提示】a_n＝（－），S_n＝（1＋－－）．

【答案】（D）．

10．等差数列｛a_n｝中，a₁＞0，S₅＝S₁₁，则第一个使a_n ＜0的项是（　　）．

（A）a₇　　（B）a₈　　（C）a₉　　（D）a₁₀

【提示】由S₅＝S₁₁ 得2 a₁＋15 d＝0，又a₁＞0，所以d ＜0．而2 a_n＝2 a₁＋2（n－1）d＝（2 n－17）d ＜0，所以2 n－17＞0即n＞8.5．

【答案】（C）．

（二）填空题（每小题5分，共30分）

11．0.98是数列｛｝中的第__________项．

【提示】令＝0.98．

【答案】n＝7．

12．已知数列｛a_n｝中，a₃，a₁₀ 是方程x²－3 x－5＝0的两根，若｛a_n｝是等差数列，则a₅＋a₈＝___________________；若｛a_n｝是等比数列，则a₆·a₇＝______________．

【提示】a₃＋a₁₀＝3，a₃a₁₀＝－5．再利用已知与所求中的关系可求．

【答案】a₅＋a₈＝a₃＋a₁₀＝3；a₆·a₇＝a₃·a₁₀＝－5．

13．在等比数列｛a_n｝中，若其中三项a₁、a₂、a₄ 又成等差数列，则公比是_____________．

【提示】由已知，得2（a₁q）＝a₁＋a₁q³ 即q³－2 q＋1＝0．

【答案】1或．

14．等差数列｛a_n｝的公差d＞0．已知S₆＝51，a₂·a₅＝52．则S₇＝_______________．

【提示】列出a₁ 和d 的方程组，求a₁ 和d ．进而求S₇ ．或由S₆＝＝3（a₂＋a₅）＝51，得方程组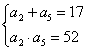，求出a₂，a₅，进而求S₇ ．

【答案】70．

15．已知数列｛a_n｝中，a₁＝－60，a_n＋1＝a_n＋3，那么a₁＋a₂＋…＋a₃₀＝_____________．

【提示】令a_n＝－60＋（n－1）×3≤0，得n≤21．所以a₁＋a₂＋…＋a₃₀＝－a₁－a₂－…－a₂₁＋a₂₂＋a₂₃＋…＋a₃₀，再求S₂₁＝，a₂₂＋…＋a₃₀＝．

【答案】765．

16．已知等差数列｛a_n｝的公差d ≠0，且a₁、a₃、a₉ 成等比数列，则＝___________．

【提示】由已知推出a₁＝d（d ≠0），并代入所求式中，消去d 即可．

【答案】．

（三）解答题（第17至19题每小题7分，第20小题9分，共30分）

17．已知数列｛a_n｝是等差数列，数列｛b_n｝的通项为b_n＝（a₁＋a₂＋…＋a_n），（n＝1，2，…）求证：数列b_n 也是等差数列．

【提示】b_n＝[na₁＋]＝a₁＋·d，再证明b_n＋1－b_n＝常数．

18．设等比数列｛a_n｝的前n 项和为S_n，若S₃＋S₆＝2 S₉ ．求数列的公比q ．

【提示】由条件可得关于q 的方程2 q⁶－q³－1＝0．

【答案】q＝－．

19．在33和25中间插入两个数，使前三个数成等差数列，后三个数成等比数列．求这两个数．

【提示】设此二数为33＋d，33＋2 d，则（33＋2 d）²＝25（33＋d）．解得d₁＝－24，d₂＝

－．

【答案】此二数为9，－15或，．

20．用若干台拖拉机耕地，若同时投入工作，耕完一片地需要24小时，但它们是每隔相等时间顺序投入工作，每一台投入工作后都工作到耕完为止，如果第一台拖拉机工作时间是最末一台工作时间的5倍，求用这种方法耕完这片土地需要的时间．

【提示】由题设知，每台拖拉机每小时的工作量是．设第一台工作时数为a₁ 小时，第二台工作时数为a₂ 小时，…，最末一台工作时数为a_n 小时，则有

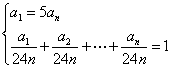，解得a₁＝40．

【答案】40小时．