向量平行的坐标表示

第九教时

教材：向量平行的坐标表示

目的：复习巩固平面向量坐标的概念，掌握平行向量充要条件的坐标表示，并且能用它解决向量平行（共线）的有关问题。

过程：一、复习：1．向量的坐标表示　 (强调基底不共线，《教学与测试》P145例三)

　　　　　　　　　　　　　　　  2．平面向量的坐标运算法则

　　　 练习：1．若M(3, -2)　N(-5, -1) 且 ,　求P点的坐标；

解：设P(x, y)　则(x-3, y+2)=(-8, 1)=(-4, )

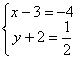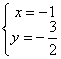　∴　　 ∴P点坐标为(-1, -)

2．若A(0, 1),  B(1, 2),　C(3, 4)　则-2=(-3,-3)

3．已知：四点A(5, 1), B(3, 4),　C(1, 3),　D(5, -3)　求证：四边形ABCD是梯形。

解：∵=(-2, 3)　 =(-4, 6)　　　 ∴=2　　　　

∴∥　且  ¹　　　 ∴四边形ABCD是梯形

二、1．提出问题：共线向量的充要条件是有且只有一个实数λ使得=λ，那么这个充要条件如何用坐标来表示呢？

2．推导：设=(x₁, y₁)　　 =(x₂, y₂)　其中¹

由=λ　　　　 (x₁, y₁) =λ(x₂, y₂)　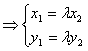　　消去λ：x₁y₂-x₂y₁=0

结论：∥ (¹)的充要条件是x₁y₂-x₂y₁=0

注意：1°消去λ时不能两式相除，∵y₁, y₂有可能为0，　∵¹

∴x₂, y₂中至少有一个不为0

2°充要条件不能写成　　　 ∵x₁, x₂有可能为0

3°从而向量共线的充要条件有两种形式：∥ (¹)

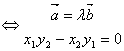
三、应用举例

例一（P111例四）　　　　　  例二（P111例五）

例三　 若向量=(-1,x)与=(-x, 2)共线且方向相同，求x

解：∵=(-1,x)与=(-x, 2) 共线　　　 ∴(-1)×2- x•(-x)=0

　 ∴x=±　　  ∵与方向相同　　 ∴x=

　例四 已知A(-1, -1) B(1,3) C(1,5) D(2,7) 向量与平行吗？直线AB与平行于直线CD吗？

　　解：∵=(1-(-1), 3-(-1))=(2, 4)　 =(2-1,7-5)=(1,2)

　　　 又：∵2×2-4-1=0　　 ∴∥

　　　 又：=(1-(-1), 5-(-1))=(2,6)　　　=(2, 4)

　　　　　2×4-2×6¹0　　 ∴与不平行

　　　 ∴A，B，C不共线　　 ∴AB与CD不重合　　　 ∴AB∥CD

四、练习：1．已知点A(0,1) B(1,0) C(1,2) D(2,1) 求证：AB∥CD

　　 2．证明下列各组点共线：1° A(1,2) B(-3,4) C(2,3.5)

　　　　　　　　　　　　　  2° P(-1,2) Q(0.5,0) R(5,-6)

　 　3．已知向量=(-1,3) =(x,-1)且∥ 求x　

五、小结：向量平行的充要条件（坐标表示）

六、作业：P112 练习 4　　习题5.4 　7、8、9　

《教学与测试》P146　　4、5、6、7、8及思考题