余弦定理

第十八教时

教材：余弦定理

目的：要求学生掌握余弦定理及其证明，并能应用余弦定理解斜三角形。

过程：一、复习正弦定理及正弦定理能够解决的两类问题。

　　　　 提出问题：1．已知两边和它们的夹角能否解三角形？

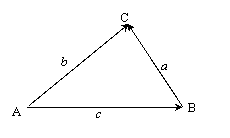　　　　　　　　　　　 2．在Rt△ABC中(若C=90°)有：　 在斜三角形中一边的平方与其余两边平方和及其夹角还有什么关系呢？

　　　 二、提出课题：余弦定理

　　　 1．余弦定理的向量证明：

　　　 　　设△ABC三边长分别为a, b, c

　 　　　=+

•=(+)•(+)=²+2•+²

 = ²+2•cos(180°- B)+²=

即：

同理可得：　　　

2．语言叙述：三角形任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍。

3．强调几个问题：1°熟悉定理的结构，注意“平方”“夹角”“余弦”等

　　　 　　　 2°知三求一

 3°当夹角为90°时，即三角形为直角三角形时即为勾股定理（特例）

4°变形：　　 　　 

三、余弦定理的应用

能解决的问题：1．已知三边求角

　　 　　　　　　　　　　　　　　　 2．已知三边和它们的夹角求第三边

例一、(P130例4)　在△ABC中，已知a=7, b=10, c=6　求A,B,C（精确到期1°）

解略

例二、(P131例5)　在△ABC中，已知a=2.730, b=3.696, C=82°28’解这个三角

形（边长保留四个有效数字，角度精确到期1’）

解略

例三、设=(x₁, y₁)　 =(x₂, y₂)　 与的夹角为q　（0≤q≤p），求证：

　　　　  x₁x₂+ y₁y₂=cosq

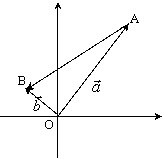证：如图：设, 起点在原点，终点为A，B

则A=(x₁, y₁)　 B=(x₂, y₂)　=-

在△ABC中，由余弦定理

-²=²+²-2 cosq

∵-²=²=(x₂-x₁, y₂-y₁)²=(x₂-x₁)²+( y₂-y₁)²

²=x₁²+y₁^{2　　　　　 2}= x₂²+y₂²

∴(x₂-x₁)²+( y₂-y₁)²= x₁²+y₁²+ x₂²+y₂²-2 cosq

∴x₁x₂+ y₁y₂=cosq　　　　  即有•= x₁x₂+ y₁y₂=cosq

四、小结：余弦定理及其应用

五、作业：P131练习　　 P132 习题5.9　　 余下部分