正、余弦函数的图象和性质
重难点知识归纳及讲解
例 1、 求下列函数的定义域
(1)y=lg(2sinx)
(2)![]()
分析:对(1)应考虑对数的真数大于0 对(2)应考虑被开方数不小于0
解答:
(1)∵2sinx﹥0
∴2kπ﹤x﹤2kπ+π(k∈Z)
∴定义域为![]()
(2)∵3cosx-1-2cos2x≥0
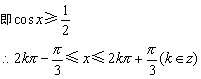
∴定义域为![]()
总结:
确定三角函数式的定义域,要注意使解析式有意义的 x满足的条件,如偶次根式内的被开方式不能小于0,分式的分母不能为0,对数的真数要大于0,底数大于0且不等于1,还要考虑三角函数本身的定义域.
例 2、 求下列函数的值域
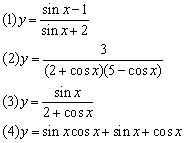
分析: 求值域要注意三角函数的有界性,即sinx≤1,cosx≤1,还需注意一些常见的变形技巧及方法.
解答: (1)![]()
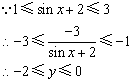 即值域为[-2,0].
即值域为[-2,0].
(2)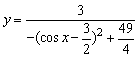 ∵-1≤cosx≤1
∵-1≤cosx≤1
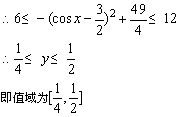
(3)原函数式可化为:
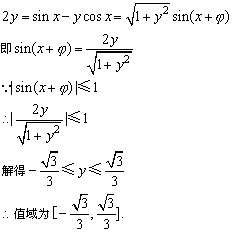
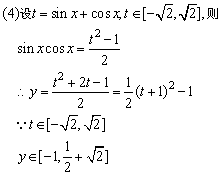
例 3 、判断下列函数的奇偶性
(1)f(x)=x2-cosx
(2)f(x)=asinx+bcosx (ab≠0)
分析:
判断奇偶性主要要看两个方面,一是函数的定义域是否关于原点对称,二是 f(-x)与f(x)之间满足什么样的关系.
解答:
(1)∵x∈R,又f(-x)=(-x)2-cos(-x)=x2-cosx=f(x) ∴f(x)是偶函数.
(2)∵x∈R,又f(-x)=asin(-x)+bcos(-x)=-asinx+bcosx≠f(x)且≠-f(x) ∴f(x)是非奇非偶函数.
例 4 、求下列函数的单调增区间
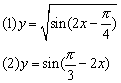
分析: 函数的增减区间是它的定义域的子集,因此均不可忽视函数定义域这一限制条件 .
解答:
(1)由![]() 得
得
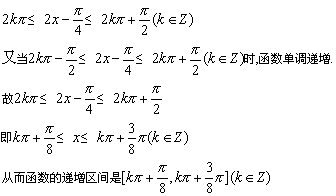
(2)![]()
∴求原函数的增区间即求![]() 的减区间
的减区间
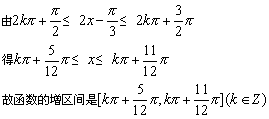
例 5、 如果函数 y=f(x)=sin2x+acox2x的图象关于直线![]() 对称,试求a的值.
对称,试求a的值.
分析一:由函数 y=Asin(ωx+φ)的图象对称轴方程的特征解题.
解答:![]()
由题意:![]() 时函数应是最大值或最小值.
时函数应是最大值或最小值.
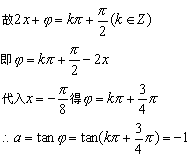
分析二:利用![]() ,再用赋值法求解. 解答:
,再用赋值法求解. 解答:![]() 是f(x)的一条对称轴.
是f(x)的一条对称轴.
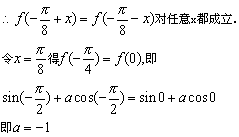
窗体顶端
一、选择题
1、函数y=-cosx的图象与余弦函数的图象( )
A.只关于x轴对称 B.只关于原点对称 C.关于原点、x轴对称 D.关于原点、坐标轴对称
2、函数y=sinx-sinx的值域是( )
A.0 B.[-1,1] C.[0,1] D.[-2,0]
3、函数![]() 的定义域是(
)
的定义域是(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4、下列四个函数中为周期函数的是( )
A.y=3 B.y=3x
C.y=sinx D.![]()
5、f(x)是以2π为周期的奇函数,且![]() (
)
(
)
A.1 B.-1
C.![]() D.
D.![]()
6、下列四个命题中,假命题是( )
A.y=cosx在![]() 上是减函数 B.y=cosx在[-π,0]上是增函数
上是减函数 B.y=cosx在[-π,0]上是增函数
C.y=cosx在第一象限是减函数 D.y=sinx和y=cosx在![]() 上都是减函数
上都是减函数
7、已知函数y=2cosx(0≤x≤2π)的图象和直线y=2围成一个封闭的图形,则这个封闭图形的面积是( )
A.4π B.2π C.8 D.4
8、函数![]() 的单调递增区间是(
)
的单调递增区间是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、函数y=-xcosx的部分图象是( )
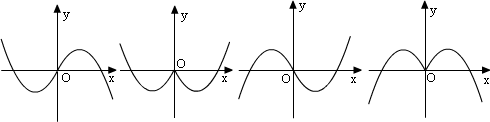 A. B. C.
D.
A. B. C.
D.
10、已知锐角α,β满足cosα﹥sinβ,则恒成立的是( )
A.α﹥β B.α﹤β
C.![]() D.
D.![]()
窗体底端
二、综合题
11、f(x)为奇函数,x﹥0时,f(x)=sin2x+cosx,则x﹤0时,f(x)=_______.
12、函数y=sin2x+cos2x的单调递减区间是____________,x=_________时,y有最大值___________.
13、求下列函数的单调增区间:
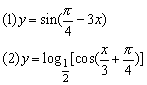
14、设函数f(x)=4cos2x(cos2x-1)+3-4cos2x (1)求使f(x)﹥0成立时x的范围.
(2)求f(x)的最大值和最小值,并求出f(x)取得最值时x的值.
15、已知![]() 求证,对x∈(0,+∞)有:
求证,对x∈(0,+∞)有: ![]()
答案:一、CDDAA CABDD
提示: 1、由图象观察.
2、![]()
3、∵sinx∈[-1,1],cos(sinx)﹥0,∴x∈ R .
4、根据周期函数的定义.
5、![]()
6、举反例,如![]() ,显然有x1﹤x2,且x1,x2都在第一象限,但cosx1﹤cosx2与y=cosx在第一象限是减函数矛盾.
,显然有x1﹤x2,且x1,x2都在第一象限,但cosx1﹤cosx2与y=cosx在第一象限是减函数矛盾.
7、![]()
8、![]() ,即求y=sin2x的增区间,且需注意sin2x﹤0,由
,即求y=sin2x的增区间,且需注意sin2x﹤0,由![]() .
.
9、由y=-xcosx是奇函数否定A、C,又当![]() 时,y﹤0否定B.
时,y﹤0否定B.
10、由cosα﹥sinβ得![]() ,故由单调性可知
,故由单调性可知![]() .
.
二、11、sin2x-cosx 提示: x﹤0时,f(x)=-f(-x)=-[sin(-2x)+cos(-x)]=sin2x-cosx
12、答案:![]() 提示:
提示:![]()
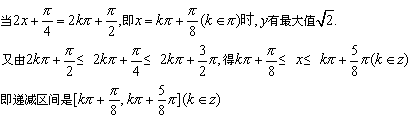
13、(1)![]() 的减区间.
的减区间.
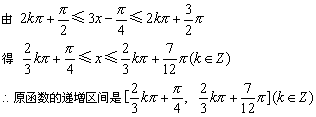
(2)由题意即求![]() ,
,
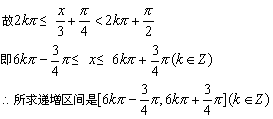
14、f(x)=4cos22x-8cos2x+3
(1)由f(x)﹥0得(2cos2x-3)(2cos2x-1)﹥0
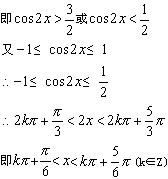
(2)f(x)=4(cos2x-1)2-1
当cos2x=1时,f(x)min=-1,此时x=kπ(k∈Z)
当cos2x=-1,即![]() 时,f(x)max=15.
时,f(x)max=15.
15、![]()