正切函数的图象和性质习题精选
一、选择题
1．函数
的最小正周期是（ ）
A．
B．
C．
D．
2．函数
的定义域是（ ）
A．
B．
C．
D．
3．函数
的值域是（ ）
A．
B．
C．
D．
4．下列函数中，同时满足①在
上是增函数；②为奇函数；③以
为最小正周期的函数是（ ）
A．
B．
C．
D．
5．已知函数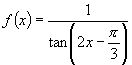
，下列判断正确的个数是（ ）
①
是定义域上的减函数，周期为
．
② 是区间
上的减函数，周期为
．
③ 是区间
上的减函数，周期为
．
④ 是区间
上的减函数，周期为
．
A．0 B．1 C．2 D．3
6．函数
的图像对称于（ ）
A．原点 B．
轴 C．
轴 D．直线
7．要得到
的图像，只需把
的图像（ ）
A．向左平移
个单位 B．向左平移
个单位
C．向右平移个单位 D．向右平移个单位
8．函数
的一个对称中心是（ ）
A．
B．
C．
D．
9．函数
的图像相邻的两支截直线
所得线段长为 ，则
的值是（ ）
A． B．0 C．1 D．－1
10．在区间
范围内，函数 与函数
的图像交点的个数为（ ）
A．1 B．2 C．3 D．4
11．要得到函数
的图像，须将函数
的图像（ ）
A．向右平移
个单位 B．向左平移 个单位
C．向右平移 个单位 D．向左平移 个单位
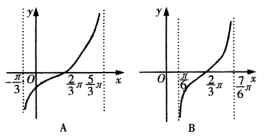
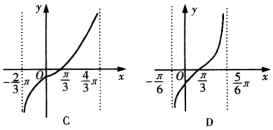
12．函数
在一个周期内的图像是（ ）
二、填空题
13．函数
的最小正周期是____________．
14．函数
的定义域是_________．
15．函数
的值域是__________．
16．已知函数
是以3为周期的奇函数，且
．若
，则
．
三、解答题
17．试求函数
的定义域，并作出区间
上的图像．
18．已知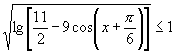
．求函数
的值域．
19．求函数
的定义域、值域，并指出它的周期、奇偶性和单调性．
20．求证：函数
（
、
）为奇函数的充要条件是
．
参考答案：
一、选择题
1．B 2．D 3．B 4．A 5．A 6．B
7．C 8．C 9．B 10．C 11．C 12．A
二、填空题
13． 14．
15．
16．－1
三、解答题
17．由
得函数的定义域为
．
又当
时，
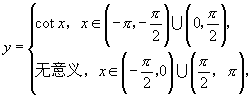
其图像如图所示．
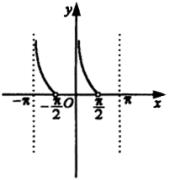
18．由已知条件得
，
解得
，
∴
（
），
∴
（ ），
∴
，
于是
．
∴当
（ ）时 取最小值4，当
（ ）时 取最大值5．从而函数的值域为［4，5］．
19．由
，得
（ ），
∴所求的函数定义域为：
；值域为
；周期为 ；
它既不是奇函数，也不是偶函数；
在区间
（ ）上是单调减函数．
20．充分性：
∵ ，
∴
为奇函数，
必要性：∵ 是奇函数．
∴
，
∴
，
∴
，
∴
，
∴
，
∴
，∴
，
∴ （ ）．