三角函数综合训练
一、 教材分析：
三角函数作为高中数学的重要内容，其变换手段丰富多彩，所涉及到的数学
想，数学方法趣味横生在高考，会考中都把考查学生驾驭数字思想方法的能力放在首位。本章涉及的数学思想和方法主要有：（1）数形结合的思想。（2）函数与方程的思想。（3）转化的思想。（4）消之的思想。（5）换元法。（6）构造法等。
二、 基础训练题：
1．选择题
(1)角α的终边与角β的终边关于y轴对称，则β为（ ）
A.-α B.л-α C.（2kл+1）л-α(k∈Z) D.kл-α（k∈Z）
(2)若sinαtgα≥0,k∈Z，则角α的集合为（ ）
A．[2kл-
，2kл+
]
B.(2kл-,2kл+)
C.(2kл-，2kл+)∪
D.以上都不对
（3）已知集合M=
，N=
则MUN等于（ ）
A．M
B.N
C.ф
D.
(4)下列四个命题中的假命题是( )
A. 存在这样的α和β的值,使得cos(α+β=cosαcosβ+sinαsinβ
B. 不存在无数个α和β的值, 使得cos(α+β)=cosαcosβ+sinαsinβ
C. 对于任意的α和β的值,使得cos(α+β)=cosαcosβ-sinαsinβ
D. 不存在这样的α和β的值,使得cos(α+β)≠cosαcosβ-sinαsinβ
(5)若cos(A+B)cos(A-B)-sin(A+B)sin(A-B)=
,A∈(0,),则tgA=(
)
A.2
B.
C.-2
D.-
(6)若sinα+cosα=
,则tgα+ctgα=( )
A.1 B.2 C.-1 D.-2
(7)已知α,β为锐角,且tgα=
,sinβ=,则α+β等于( )
A.
B.
C
D.
(8)已知sinα+sinβ=1,cosα+cosβ=0,那么cos2α+cos2β等于( )
A.1
B.
C.
D.
(9)当0＜x＜л时,则方程cos (лcosx)=0的解集为( )
A. 
B.
C.
D.
(10)下列四个值:sin3,cos3,tg3,ctg3的大小关系是( )
A.cos3＜tg3＜ctg3＜sine B.sin3＞cos3＞tg3＞ctg3
C.ctg3＜tg3＜cos3＜sin3 D.sin3＞tg3＞cos3＞ctg3
(11)已知＜α＜л＜,sinα=
,则cos
的值为( )
A.
或-
B.- C.
D.以上都不对
(12)在△ABC中,角A、B、C的对边分别为a、b、c，已知c=3,∠C=60°,a+b=5,则
等于（ ）
A．
B.
C.
D.
(13)△ABC中,A=60°,b=1,这个三角形的面积为
,则△ABC外接圆的直径为( )
A.
B.
C.
D.
(14)在Rt△ABC中,C=90°,则sinAcos2(45°-
)-sin
cos
A.有最大值
和最小值0
B.有最大值但无最小值
C.即无最大值也无最小值
D.有最大值但无最小值
(15)函数y=
在区间(0,л)上的最小值为( )
A.
B.2
C.1
D.
(16)若0≤x≤,则y=
sinx+3cosx的最小值是( )
A.1
B.2
C. D.0
(17)已知函数f (x)=3sin2
+1,使得f (x+c)=f (x)成立c的最小正整数为( )
A.1 B.2 C.4 D.以上都不对
(18)若θ是第四限的角,且sinθ=-,那么2θ是( )
A.第一象限的角 B.第二象限的角 C.第三象限的角 D.第四象限的角
(19)函数y=
的值是( )
A.y≤ B.-4≤y≤ C.y≥-4 D.-4＜y≤
(20)要得到y=sin2x的图象,只需将y=cos(2x-)的图象 ( )
A.向右平移
B.向左平移
C.向右平移 D.向左平移
(21)函数y=cos2(x-
+sin2(x+)-1是( )
A.周期为2л的奇函数 B．周期为л的偶函数
C.周期为л的奇函数 D.周期为2л的偶函数
(22)设方程cos2x+sin2x=α+1,d [0,]上有两个不同的实数角,则α的取值范围是( )
A.[-3,1] B.[-л1] C.[0,1] D.[0,1]
2.填空题:
(1)已知θ=
,则tg
= .
(2)计算sin
sin
=
.
(3)若f (tgx)=
,则f (ctgx)=
.
(4)已知α=arcsin
则cos2α=
.
(5)在△ABC中,sin
=
,则△ABC的形状为
．
(6)直角三角形的周长为定值2l,则斜边的最小值是 .
(7)已知sin(+α)sin(-α)=
,α∈(,л),则sin4α=
.
(8)已知x∈(0, ),则下面四式:
①sinx＜x＜tgx ②sin(cosx)＜cosx＜cos(sinx)
③sin3x+cos3x＜1 ④cos(sinx)＜sin(cosx)＜cosx中正确命题的序号是 .
(9)
.
(10)[2sin50°+sin10°(+tg10°)]
=
.
3.解答题
(1) 求函数y=2cosθsinθ-cosθ-sinθ(θ∈[0,л])的值域
(2) 已知tgα=log3525,tgβ=log725,求2sin(α-β)+sinα+sinβ的值
(3) 改sinA=asinB,cosA=bcosB,A、B为锐角且a＞1,0＜b＜1，求tgAr的值
(4) 已知0＜α＜л，0＜β＜л，tgαtgβ是方程x2+5x+6=0的两根。
①求α+β的值；
②求cos(α-β)的值.
(5)在锐角△ABC∠A＜∠B＜∠C,且B=60°,
=
,求证：a+
(6)在Rt△ABCk ，C=90°，r、R分别为三角形内切圆与外接圆的半径，求
的最大值.
(7)设sinx+siny=sinx·siny,tg
,求sin
的值.
(8)若x1、x2是方程x2-sin·cosл=0的两根，且α=arctgx1β=arctgx2,求α+β.
(9)若常数α满足
＜1,求使函数f
(x)=sin(x+α)+cos(x-α)为偶函数的α的值.
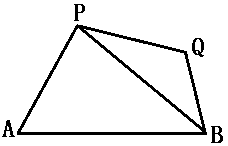
(10)如图,在平面有点A、B、P、Q，其中
，
设△APB与△PQB面积为S、T，求S2+T2的取值范围.
第五单元 三角函数综合训练
1． 选择题
C C B B C B B C B D C BＣＢＤ ＣＢＣＤＡ C D
2． 填空题
（1） （2） （3）
（4）-
（5）正三角形 （6）2l（-1）
（7）-
（8）①②③ （9）32 （10）
3． 解答题
（1）
解：令t=sinθ+cosθ 则-
≤t≤1
∴2sinθcosθ=t2-1
∴y=t2-t-1=(t-)2-
∴y∈[-,1]
(2)原式=2sinαcosβ+sinαsinβ-2cosαsinβ
=cosαcosβ(2tgα+tgαtgβ-2tgβ)
=cosαcosβ(2tg3525+log3525·log725-2log725)
=cosαcosβ[4log355+4log355·log75-4log75]
=cosαcosβ[4log355(1+log75)-4log75]
=cosαcosβ[4log355 ·log735-4log75]
=cosαcosβ(4log75-4log75)
=0
(3)解由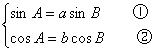
①2+②2得a2sin2B+b2cos2B=1
∴cos2B=
∴sin2B=
∴tg2B=
∵B为锐角 ∴tgB=
得tg A=
tgB=
(4)解略：（1）α+β的值为
( 2 ) cos (α+β)=
(5)解：∵B=60° ∴A+C=120° cos(A+C)=-
又由已知
=
∴cosAcosC=
sinAsinC=
∴cos(C-A)= 即C-A=30°
∴A=45° B=60° C=75°
∴a+b=2R(sin45°+sin60°)
=2·2R
=2·2Rsin75°
=2C
(6)解：∵2R=AD+DB AD=rtg
BD=rtg
∴2R=r(tg+tg)
∴ =
=
=
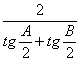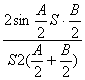
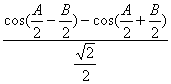
=[cos(
)-]
≤
故当A=B时 有最大值
（7）解：由sinx+siny=sinxsiny可得
2sin
=-[cos(x+y)-cos(x-y)]
=-[(1-2sin2)-(2cos2
)-1]
=-1+sin2
∴(sin
)2=1
∴sin=±1
再由tg知cos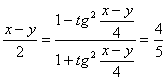
∴sin
(
＞1舍去)
（8）解：∵x1、x2是方程x-sin x1、x2
∴tg(α+β)=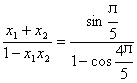
=
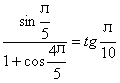
又由题意α、β中有一个在这间（-，0）内
∴-＜α+β＜ ∴α+β=
(9)解：由＜1 知
-1＜logл
＜1 即1＜α＜л2
要使f (x)为偶数，必须f (-x)=f (x)
即x∈R恒成立
移项 和差化积得
2sinxcosα=-2sinxsinα
若对x∈R恒成立
必须：tgα=-1 ∴α=kл+ (k∈z)
于是 1＜kл+＜л2
知 k=0，1，2
∴α=，
，
（10）解：设∠BAP=α α∈[0,]
∠BQP=β,在△PAB,△PBQ中
由余弦定理cosβ=cosα-1
∴S2+T2=(sinα)2+(sinβ)2
=-(cos-
)2+
∴当cosα=1时，S2+T2有最小值
当cosα=时，S2+T2有最大值