三角函数综合训练卷A
(120分钟,满分150分)
一、选择题(每题5分,共60分)
1.设2θ是第一象限角,那么( )
A.sinθ>0 B.cosθ>0
C.tanθ>0 D.cotθ<0
2.若θ为第二象限的角,![]() 的值等于( )
的值等于( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.若角α,β的终边关于y轴对称,则下列等式成立的是( )
A.sinα=sinβ B.cosα=cosβ
C.tanα=tanβ D.cotα=cotβ
4.若α是第四象限的角,且![]() ,则
,则![]() 是( )
是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.已知A为三角形内角,且![]() ,则cosA-sinA的值是( )
,则cosA-sinA的值是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.若sinα+cosα=1,则sinα-cosα的值为( )
A.1 B.-1
C.±1 D.0
7.已知α+β=3π,下列等式恒成立的是( )
A.sinα=sinβ B.cosα=cosβ
C.tanα=tanβ D.cotα=cotβ
8.已知sinα=0,则不是α的解集的是( )
A.{αα=kπ,k∈Z}
B.{αα=2kπ或(2k+1)π,k∈Z}
C.![]()
D.{αα=(k-2)π,k∈Z}
9.已知![]() ,
,![]() ,则角x等于( )
,则角x等于( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.若![]() ,则角x等于( )
,则角x等于( )
A.![]() ,
,![]()
B.2kπ,![]() (k∈Z)
(k∈Z)
C.![]()
D.![]()
11.函数![]() 的定义域是( )
的定义域是( )
A.![]() (k∈Z)
(k∈Z)
B.![]() (k∈Z)
(k∈Z)
C.![]() (k∈Z)
(k∈Z)
D.![]() (k∈Z)
(k∈Z)
12.角α(0<α<2π)的正弦线与余弦线相等,且符号相同,那么α的值为( )
A.![]() 或
或![]()
B.![]() 或
或![]()
C.![]() 或
或![]()
D.![]() 或
或![]()
二、填空题(每题4分,共16分)
13.已知sinα与cosα是方程![]() 的两根,则m=___________。
的两根,则m=___________。
14.若![]() ,则sinθ+cosθ=___________。
,则sinθ+cosθ=___________。
15.若![]() ,α∈R则α=___________。
,α∈R则α=___________。
16.若![]() ,且-2π<x≤0,则x=___________。
,且-2π<x≤0,则x=___________。
三、解答题(共74分)
17.已知tanα+cotα=m,求sinα+cosα的值。(10分)
18.已知:![]() ,求
,求![]() 的值。(12分)
的值。(12分)
19.求适合![]() 的x的集合。(12分)
的x的集合。(12分)
20.若α为锐角,求证:sinα<α<tanα。(12分)
21.已知![]() ,
,![]() ,且
,且![]() ,0<β<π,求角α,β。(14分)
,0<β<π,求角α,β。(14分)
22.已知x,y都是实数,且![]() ,求
,求![]() 的值。(14分)
的值。(14分)
参考答案
一、1.C2.A3.A4.B5.D
6.C7.A8.C9.C10.C
11.A12.C
二、13.![]()
14.±1
15.![]() 或
或![]() ,k∈Z}
,k∈Z}
16.![]() 或
或![]()
三、17.解:∵tanα+cotα=m
∴![]()
∴![]()
又∵![]()
∴![]()
18.解:∵![]()
∴![]()
19.解:由![]() 得
得![]()
由![]() 得
得![]()
由![]() 得
得![]() 或
或![]()
∴所求的x的集合为![]() 或
或![]()
20.证明:在单位圆中![]() ,MP=sinα AT=tanα
,MP=sinα AT=tanα
∵![]() ,
,
![]() ,
,![]() ,
,
![]()
∴![]() ,
,
∴sinα<α<tanα
21.解:∵![]() ,且
,且![]() ,
,
∴![]()
又∵![]()
∴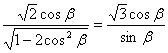
∴![]() 即
即
![]()
∴![]()
∴![]() 当
当![]() 时,
时,![]()
当![]() 时,
时,![]()
又∵![]() ,0<β<π
,0<β<π
∴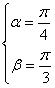 或
或
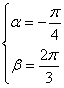
22.解:∵![]()
∴x-6=0,y+2=0,即x=6,y= -2,
∴原式![]()
![]()
[解题点拨]
1.由2θ是第一象限角,知θ角在一、三象限,这样就可分类确定各三角函数值的符号;已知α在第二象限则![]() 在一、三象限,已知α在三、四象限时,
在一、三象限,已知α在三、四象限时,![]() 在二、四象限。对一些常用的结论,虽不是以定理、公式的形式出现,也应通过练习去掌握它们,会对完成习题提供有利的时间。
在二、四象限。对一些常用的结论,虽不是以定理、公式的形式出现,也应通过练习去掌握它们,会对完成习题提供有利的时间。
2.因为![]() ,又θ在第二象限角,sinθ>0且
,又θ在第二象限角,sinθ>0且![]() ,所以直接利用公式,在利用公式或定理解题时,一定要注意公式或定理的使用条件。
,所以直接利用公式,在利用公式或定理解题时,一定要注意公式或定理的使用条件。
3.因为α,β的终边关于y轴对称,所以在α,β的终边上关于y轴对称的点的纵坐标不变,横坐标互为相反数;然后再利用任意角的三角函数定义判断。
5.因为![]() ,所以
,所以![]() ;此时还要注意A是三角形的内角,
;此时还要注意A是三角形的内角,![]() ,所以A是第二象限角,sin>0即cosA-sinA<0;解题时要注意已知条件对结论的限制,要审清题目中的所有已知条件。
,所以A是第二象限角,sin>0即cosA-sinA<0;解题时要注意已知条件对结论的限制,要审清题目中的所有已知条件。
9.解此题的一般方法是通过![]() ,求出满足条件的x的集合然后用
,求出满足条件的x的集合然后用![]() 去排除,此题所给的选项都是具体的角,故可以采用逐一代入排除较为简单;特殊作法在做选择题过程中经常用到,故要注意审题。
去排除,此题所给的选项都是具体的角,故可以采用逐一代入排除较为简单;特殊作法在做选择题过程中经常用到,故要注意审题。
12.首先要掌握正、余弦线的定义,并明确其方向的确定方法;由题意知,α角可能在一或三象限。
13.由根与系数的关系得![]() ①,
①,![]() ②
②
通过![]() ,把②代入即可求出m值;在三角运算、求值、证明过程中,往往要利用同角三角函数的关系进行过渡,所以要根据题目需要,注意选择关系式。
,把②代入即可求出m值;在三角运算、求值、证明过程中,往往要利用同角三角函数的关系进行过渡,所以要根据题目需要,注意选择关系式。
14.由![]() ,得
,得![]() ,然后先求
,然后先求![]() ,所以sinθ+cosθ=±1;解题的关系还是
,所以sinθ+cosθ=±1;解题的关系还是![]() 的运用。
的运用。
15.由![]() ,可得α角的终边与
,可得α角的终边与![]() 角的终边相同或关于y轴对称,然后分别写出α角的范围;对于已知三角函数值,求已知角,应先求出0°~360°之间满足条件的角,再根据题意写出角的集合。
角的终边相同或关于y轴对称,然后分别写出α角的范围;对于已知三角函数值,求已知角,应先求出0°~360°之间满足条件的角,再根据题意写出角的集合。
16.利用诱导公式化简![]() 得
得![]() ,角x的终边将在一或二象限,先求出0°≤x<360°间满足条件的角,再写出-2x<x≤0内的角。
,角x的终边将在一或二象限,先求出0°≤x<360°间满足条件的角,再写出-2x<x≤0内的角。
17.把tanα与cotα分别用正弦,余弦表示,再通分相加,即可求出sinα·cosα的值,先求![]() 的值,后开方就可以求出所求结果;解三角化简问题时,尽量把正切、余切表示成正弦、余弦,这样容易找到突破口。
的值,后开方就可以求出所求结果;解三角化简问题时,尽量把正切、余切表示成正弦、余弦,这样容易找到突破口。
18.化简![]() ,因为
,因为![]() ,所以
,所以
![]() 。
。
本题主要考查整体代入的方法及三角概念及公式的推广。
19.通过方程思想解出![]() ,然后分类求解;本题两次应用分类讨论的数学思想,解题时不要漏掉任何一种情况。
,然后分类求解;本题两次应用分类讨论的数学思想,解题时不要漏掉任何一种情况。
20.利用单位图,把α、sinα、tanα都用线段或弧长表示,然后利用三角形的面积关系进行判断;在比较同角或不同角的各三角函数大小时,往往利用单位图中对应三角线来比较较为简单,同时要注意三角线是具有方向的线段。
21.因为![]() ,所以可用cosβ表达或表示cosα,并代入
,所以可用cosβ表达或表示cosα,并代入![]() 中即可求解。此类型题目,就是先由条件求出各角的三角函数值,再求角。
中即可求解。此类型题目,就是先由条件求出各角的三角函数值,再求角。
22.由已知条件求x,y的值,然后代入求值;本题考查的是三角知识点与初中求代数减式值问题的综合运用。