三角函数总测试
测试卷（120分钟，满分150分）
一、选择题（每题5分，共60分）
1．若角α的终边落在直线y=-x上，则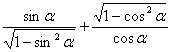
的值等于（ ）
A．0 B．2
C．-2 D．2tgα
2．设θ∈（0，2π），若sinθ＜0且cos2θ＜0，则θ的取值范围是（ ）
A．
B．
C．
D．
3．函数
的这天义域是（ ）
A．
（k∈Z）
B．
（k∈Z）
C．
（k∈Z）
D．
（k∈Z）
4．函数
的值域是（ ）
A．[0，8] B．[-3，5]
C．
D．[-4，5]
5．已知α，β∈
，cosα+sinβ＞0，则（ ）
A．α+β＜π
B．
C．
D．
6．已知tanα，tanβ是方程
的两根，且α，β∈
，则α+β等于（ ）
A．
B．或
C．
或
D．
7．有四个函数：①
②y=sinx③
④y=sinx，其中周期是π，且在
上是增函数的函数个数是（ ）
A．1 B．2
C．3 D．4
8．函数
的最小正周期是（ ）
A．π B．2π
C．
D．
9．
是tanx=1成立的（ ）
A．充分非必要条件
B．必要非充分条件
C．充要条件
D．既非充分条件也非必要条件
10．设
，
，
则（ ）
A．a＜b＜c B．a＜c＜b
C．b＜c＜a D．c＜b＜a
11．把函数
的图象向左平移m个单位，所得的图象关于y轴对称，则m的最小值是（ ）
A．
B．
C．
D．π
12．已知函数
，
，那么函数
的振幅A的值是（ ）
A．5 B．7
C．
D．13
二、填空题（每题4分，共16分）
13．函数
的最小正周期是_____________。
14．已知
，α，β∈R，则
的取值范围是_____________。
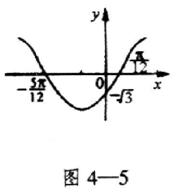
15．已知函数y=Asin（ωx+
）（A＞0，ω＞0，0≤＜2π）的图象如图4-5所示，则这个函数的解析式为y=_____________。
16．给出以下五个命题：①存在实数α，使sinαcosα=1；②存在实数α，使
；③函数
是偶函数；④直线
是函数
的图象的一条对称轴；⑤若α，β都是第一象限角，且α＞β，则tanα＞tanβ，其中正确的命题序号是_____________。
三、解答题（共74分）
17．若sinαcosα＜0，sinαtanα＜0。化简：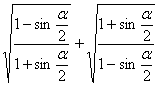
。（10分）
18．已知函数
。
（1）求f（x）的最小正周期；
（2）求f（x）的最大值与最小值；
（3）求f（x）图象的对称轴；
（4）求f（x）的递增区间。（12分）
19．设
，
。求：
（1）
；
（2）tanθ-cotθ。（12分）
20．已知
，
且α∈（0，π），β∈（0，π），求2πα-β的值。（12分）
21．已知
，
，求cos（α+β）的值。（14分）
22．已知奇函数f（x）在（-∞，0）∪（0，+∞）上有意义，且在（0，+∞）上是增函数，f（1）=0，又函数
， m∈
，若集合M={mg（θ）＜0}，集合N={mf[g（θ）] ＜0＝，求M∩N。（14分）
参考答案
一、1．A2．B3．C4．D5．D
6．D7．C8．B9．D10．B
11．C12．C
二、13．
14．
15．
16．③④
三、17．因为sinαcosα<0 sinαtgα<0，
所以α为第二象限角，
即
，
故
，
即
是第一或第三象限角，
原式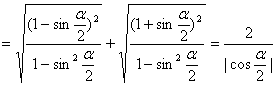
。
当是第一象限角时，原式=
，当是第三象限角时，
原式
。
18．
。
（1）
；
（2）A=2，故
，
；
（3）由
得
，即f（x）的对称轴是直线
。
（4）由
得
，
即f（x）的递增区间是
（k∈Z）
19．因为，
故
，
，
故
。
又，sinθ>0 cosθ<0，
所以sinθ-cosθ>0，
而
，
所以
，
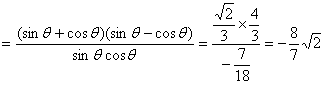
20．因为，
所以
又，0<α<π故
再由，0<β<π知
∴
，在
上只有一个
的正切值等于1。
21．由已知得
，
。
故
，
。
从而
，
所以
。
22．依题意，f（-1）=-f（1）=0，又f（x）在（0，+∞）上是增函数，
所以f（x）在（-∞，0）上也是增函数，
因此，由f(x)<0得x<-1或0<x<1。
所以N={m f[g（θ）]<0}={m g（θ)<-1或0<g（θ)<1}，
M∩N={m g（θ）<-1}，
由g（θ）<1得
，
即
，
所以
，
设cosθ-2=t，
则当
时，t∈[-2，-1]，
（可以证明
在
上是增函数，
在
上是减函数，由此知
时可以取到等号）。
从而
。
所以
即
。
[解题点拨]
1．α的终边在第二象限或第四象限。
2．
，
，取交集可得。
3．
，
，k∈Z。
4．
5．
，
由α，β∈，
故
，即。
6．注意该方程两根均为负实数，由此可得α、
7．
，T=π在（0，2π）上是增函数，
y=sinx，T=π在上是增函数，
，
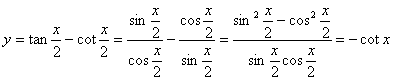T=π在上是增函数，y=sinx不是周期函数。
8．
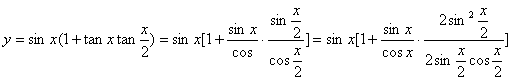
9．
时，但tgx≠1，
时，tgx=1
但
10．a=sin24°，
，
。
11．
。
依题意
，
，k∈Z，m>0，
故
。
12．
。
。
13．
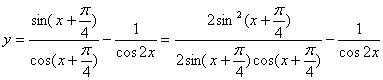
14．由得
或sinα=1，
，故
。
15．
，
，
，
故
。