三角同步测试

三角同步测试

窗体顶端

一、选择题

1、在下列各组角中，终边不相同的一组是（ ）

A．60°与－300°　　　　　　　　　　　　B．230°与950°

C．1050°与－300°　　　　　　　　　　　D．－1000°与80°

2、下列命题中，真命题是（ ）

A．第一象限角是锐角

B．第二象限角比第一象限角大

C．角α是第四象限角的充要条件是k·360°－90°<α<k·360°，k∈Z

D．三角形的内角是第一或第二象限角

3、经过3小时35分钟，时针与分针转过的度数之差是（ ）

A．1182.5°　　　　　　　　　　　　　　　B．－1182.5°

C．1182.3°　　　　　　　　　　　　　　　D．－1182.3°

4、已知，则点P（cosα，sinα）所在象限是（ ）

A．第一象限　　　　　　　　　　　　　　　B．第二象限

C．第三象限　　　　　　　　　　　　　　　D．第四象限

5、已知，则（ ）

A．M=N　　　　　　　　　　　　　　　　　　B．MN

C．MN　　　　　　　　　　　　　　　　　D．M∩N=

6、一弓形的弧所对圆心角是60°，弓形的弦长为2cm，则弓形的面积为（ ）

A．　　　　　　　　　　　　　B．

C．　　　　　　　　　　　　　　D．

7、已知角θ终边经过点P（3a，4a）（a≠0），则下列式子中正确的是（ ）

A．sinθ=　　　　　　　　　　　　　　　　B．secθ=

C．tanθ=　　　　　　　　　　　　　　　　 D．cotθ=－

8、在[0，2π]上满足sinx≥的x的取值范围是（ ）

A．[0，]　　　　　　　　　　　　　　　B．

C．　　　　　　　　　　　　　　D．

9、设角α是第二象限角，且，则是（ ）

A．第一象限角　　　　　　　　　　　　　　　B．第二象限角

C．第三象限角　　　　　　　　　　　　　　D．第四象限角

10、已知E={θcosθ<sinθ，0≤θ≤2π}，F={θtanθ<sinθ}.则E∩F为（ ）

A．　　　　　　　　　　　　　　　　B．

C．　　　　　　　　　　　　　　D．

窗体底端

二、填空题

11、已知角θ的终边上有一点P（－，y）（y≠0）且sinθ=，则cosθ=___________.

12、若A={αα=60°＋k·360°，k∈Z}，B={αα=60°＋k·180°，k∈Z}，C={αα=60°＋k·720°，k∈Z}，则A、B、C的关系是___________.

13、设f(x)=sinx，则f(1)＋f(2)＋f(3)＋…＋f(2005)=___________.

三、解答题

14、已知f(x)=5°·x＋20°，g(x)=6°x＋30°，问T为何值时，对任意x值均有f(x＋T)与f(x)，g(x＋T)与g(x)同时终边相同？

15、若θ在第四象限，试判断sin(cosθ)·cos(sinθ)的符号.

16、若α，β是关于x的二次方程，x²＋2(cosθ＋1)x＋cos²θ=0的两根，且α－β≤2，求θ的范围.

答案：一、1---5CCBBC,　6---10ACBCA

二、11、－

^{解：由三角函数的定义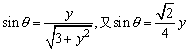，故y2=5.}

∴.

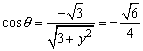12、CAB

解析： A={αα=2k·180°＋60°，k∈Z}，∴ AB

　C={αα=2k·360°＋60°，k∈Z}，∴ CA，故CAB.

13、

提示：从特殊看起，可得到 f(1)=f(7)，f(2)=f(8)，f(3)=f(9)，…

　∴

　f(1)＋f(2)＋…＋f(2005)=[f(1)＋f(2)＋…＋f(6)]×334＋f(2005)

　而 f(1)＋f(2)＋f(3)＋f(4)＋f(5)＋f(6)=.

　∴ f(1)＋f(2)＋…＋f(2005)=f(2005)=f(1)=.

三、14、解析：∵ f(x＋T)与f(x)终边相同.

　∴ 5°(x＋T)＋20°=5°·x＋20°＋k·360°

　即 T=72k。

　又∵ g(x＋T)与g(x)终边相同，

　∴ 6°·(x＋T)＋30°=6°x＋30°＋k′·360°.

　即 T=60k′。

　由于 60和72的最小公倍数是360，故T=360k（k∈Z）.

15、解析：∵ θ在第四象限，∴ 0<cosθ<1<，－<－1<sinθ<0，

　∴ sin(cosθ)>0，cos(sinθ)>0

　∴ sin(cosθ)·cos(sinθ)>0.

16、解析：由△=4(cosθ＋1)²－4cos²θ≥0得cosθ≥－。

　又α＋β =－2(cosθ＋1)，α·β=cos²θ

　

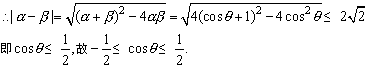
　利用三角函数线可得（k∈Z）.