第五教时
教材：实数与向量的积
目的：要求学生掌握实数与向量的积的定义、运算律，理解向量共线的充要条件。
过程：一、复习：向量的加法、减法的定义、运算法则。
二、1．引入新课：已知非零向量
作出++和(-)+(-)+(-)
 |  | ||
=
=++=3
=
=(-)+(-)+(-)=-3
讨论：1°3与方向相同且3=3
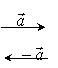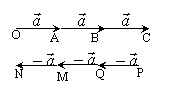2°-3与方向相反且-3=3
2．从而提出课题：实数与向量的积
实数λ与向量的积，记作：λ
定义：实数λ与向量的积是一个向量，记作：λ
1°λ=λ
2°λ>0时λ与方向相同；λ<0时λ与方向相反；λ=0时λ=
3．运算定律：结合律：λ(μ)=(λμ)
①
第一分配律：(λ+μ)=λ+μ
②
第二分配律：λ(+
)=λ+λ
③
结合律证明：
如果λ=0，μ=0，=至少有一个成立，则①式成立
如果λ¹0，μ¹0，¹有：λ(μ)=λμ=λμ
(λμ)=λμ =λμ
∴λ(μ)=(λμ)
如果λ、μ同号，则①式两端向量的方向都与同向；
如果λ、μ异号，则①式两端向量的方向都与反向。
从而λ(μ)=(λμ)
第一分配律证明：
如果λ=0，μ=0，=至少有一个成立，则②式显然成立
如果λ¹0，μ¹0，¹
当λ、μ同号时，则λ和μ同向，
∴(λ+μ)=λ+μ=(λ+μ)
λ+μ=λ+μ=λ+μ=(λ+μ)
∵λ、μ同号 ∴②两边向量方向都与同向
即：(λ+μ)=λ+μ
当λ、μ异号，当λ>μ时 ②两边向量的方向都与λ同向
当λ<μ时 ②两边向量的方向都与μ同向
还可证：(λ+μ)=λ+μ
∴②式成立
第二分配律证明：
如果=，=中至少有一个成立，或λ=0，λ=1则③式显然成立
当¹，¹且λ¹0，λ¹1时
1°当λ>0且λ¹1时在平面内任取一点O，
作
λ 
λ
则
+
λ+λ
由作法知：
∥
有ÐOAB=ÐOA1B1 =λ
∴
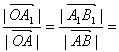λ ∴△OAB∽△OA1B1
∴
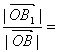λ ÐAOB=Ð
A1OB1
因此，O，B，B1在同一直线上，
=λ
与λ方向也相同
λ(+)=λ+λ
当λ<0时 可类似证明：λ(+)=λ+λ
∴ ③式成立
4．例一 （见P104）略
三、向量共线的充要条件（向量共线定理）
1．若有向量(¹)、，实数λ，使=λ 则由实数与向量积的定义知：与为共线向量
若与共线(¹)且：=μ，则当与同向时=μ
当与反向时=-μ
从而得：向量与非零向量共线的充要条件是：有且只有一个非零实数λ
使=λ
2．例二（P104-105 略）
三、小结：
四、作业： 课本 P105 练习 P107-108 习题5.3 1、2