实数与向量的积综合练习

第七教时

教材：5.3实数与向量的积综合练习《教学与测试》P141-144 67、68课

目的：通过练习使学生对实数与积，两个向量共线的充要条件，平面向量的基本定理有更深刻的理解，并能用来解决一些简单的几何问题。

过程：一、复习：1．实数与向量的积　(强调：“模”与“方向”两点)

　　　　　　　　　　　　　　 　 2．三个运算定律（结合律，第一分配律，第二分配律）　　

　　　　　　　　　　　　　  3．向量共线的充要条件

　　　　　 　　　　　　　　 4．平面向量的基本定理（定理的本身及其实质）

二、处理《教学与测试》

1．当λÎZ时，验证：λ(+)=λ+λ

证：当λ=0时，左边=0•(+)=　右边=0•+0•=　分配律成立

　当λ为正整数时，令λ=n,　则有：

n(+)=(+)+(+)+…+(+)

=++…+++++…+=n+n

即λ为正整数时，分配律成立

当为负整数时，令λ=-n（n为正整数），有

-n(+)=n[-(+)]=n[(-)+(-)]=n(-)+n(-)=-n+(-n)=-n-n

分配律仍成立

综上所述，当λ为整数时，λ(+)=λ+λ恒成立 。

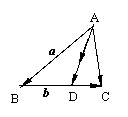
2．如图，在△ABC中，=, =　　 AD为边BC的中线，G为△ABC的重心，求向量

　　　 解一：∵=, =　 则==

∴=+=+而=

∴=+

　　　　　　　　　　　　　　　　　　  解二：过G作BC的平行线，交AB、AC于E、F

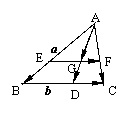　　　　　　　　　　　　　　　　　　　　　　　　 ∵△AEF∽△ABC

　　　　　　　　　　　　　　　　　　　　　　　　 ==　　==

　　　　　　　　　　　　　　　　　　　　　　　　 ==

　　 　　　　　　　　　　　　　　　　　∴=+=+

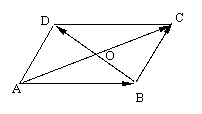
　 3．在　　 ABCD中，设对角线=，=试用, 表示，

　　　　 解一：==　　　　　　 ==

∴=+=-=-

 =+=+=+

　　　　 解二：设=，=

则+=　　　　　　 +=　　　　 ∴　=(-)

　 -=　　　　　　  -=　　　　　　　  =(+)

　　 即：=(-)　　　 =(+)

　4．设,　是两个不共线向量，已知=2+k,　=+3, =2-, 若三点A, B, D共线，求k的值。

解：=-=(2-)-(+3)=-4

∵A, B, D共线　　　∴,共线　  ∴存在λ使=λ

即2+k=λ(-4)　　　 ∴　　  　 ∴k=-8

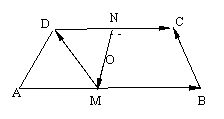
5．如图，已知梯形ABCD中，AB∥CD且AB=2CD，M, N分别是DC, AB中点，设=, =，试以, 为基底表示, ,

　　　　　　　　　　　　　　　　　　　　　  解：==　　连ND 则DC╩ND

　　　　　　　　　　　　　　　　　　　　　　　　　 ∴==-=-

　　　　　　　　　　　　　　　　　　　　　　　　　 又：==

　　　　　　　　　　　　　　　　　　　　　　　　　 ∴=-=-=--

=(-+)-=-

6．1kg的重物在两根细绳的支持下，处于平衡状态（如图），已知两细绳与水平线分别成30°, 60°角，问两细绳各受到多大的力？

解：将重力在两根细绳方向上分解，两细绳间夹角为90°

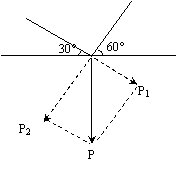
=1 (kg)　 ÐP₁OP=60°　　 ÐP₂OP=30°

∴=cos60°=1•=0.5　  (kg)

=cos30°=1•=0.87　  (kg)

　 即两根细绳上承受的拉力分别为0.5 kg和0.87 kg

三、作业：《教学与测试》67、68课练习