第二十四教时
教材：复习三——平面向量的坐标运算、定比分点
过程：
一、复习：平面向量坐标的概念，运算法则，定比分点
二、 例题：
1．已知四边形的顶点坐标为A(1,2)，B(2,5)，C(8,14)，D(3,5)，
求证：四边形ABCD是一个梯形。
证：∵
=(2,3), 
=(6,9) 且2×9-3×6=0 ∴∥
又∵
=(1,3), 
=(-5,-9) 而1×(-9)-3×(-5)¹0 ∴∥
∴ABCD为梯形
2．设a = (1,x)，b = (-1,3)，且2a + b∥a -2b，试求x。
解：2a + b = (1,), a -2b = (3, x-6)
∵2a + b∥a -2b ∴1×(x-6) - (2x+3)×3 = 0 Þ x = -3
3．已知：A(1,-2)，B(2,1)，C(3,2)，D(-2,3)，
1°求证：A，B，C三点不共线
2°以、
为一组基底来表示+
+
解：1°∵=(1,3), =(2,4) ∵1×4-3×2¹0 ∴
∴A，B，C三点不共线
2°++=(-3,5)+(-4,2)+(-5,1) = (-12,8)
设：++= m+ n
即：(-12,8) = (m + 2n, 3m + 4n)
∴
∴++= 32-22
4．已知M(1,-3)，N(4,6)，P(x,3)，且三点共线，求点P分有向线段MN所成的比λ及x的值。
解：
解得：λ= 2, x = 3
5．
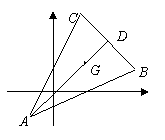已知△ABC的顶点是A(x1, y1)，B(x2, y2)，C(x3, y3)，求△ABC的重心G的坐标(x, y)。
解：如图：∵D是BC中点，
∴D点的坐标(
)
且G分有向线段AD所成的比λ=2
∴G的坐标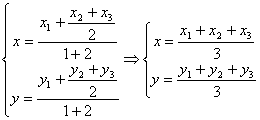
∴△ABC的重心G的坐标是(
)
6．
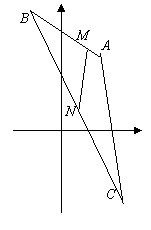已知A(1,2)，B(-1,3)，C(2,-2)，点M分
的比λ为3:1，点N在线段BC上，且
，求点N的坐标。
解：由题设：
=3
∴=
又： ∴
即：
sinÐABC =
•sinÐABC
又 = ∴ = 
∴=
即N分的比为4:5, 设N(x, y)
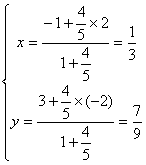∴点N的坐标是
7．已知点M(2,3)，N(8,4)，点P在线段MN上，且
，
求点P坐标和λ。
解：设点P坐标为(x, y)，由
，
，
又∵
可知λ¹ 0，且
，
从而
, ∴
∴
∴
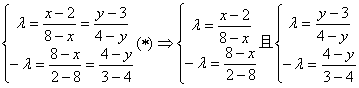
代入检验(*)：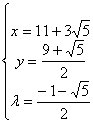
或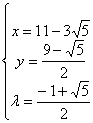
∴点P坐标
或点P坐标
三、 作业： 《导学•创新》 §5.4 §5.5