平面向量基本定理

第六教时

教材：平面向量基本定理

目的：要求学生掌握平面向量的基本定理，能用两个不共线向量表示一个向量；或一个向量分解为两个向量。

过程：一、复习：1．向量的加法运算（平行四边形法则）。

　　　　　　　　　　　　　　 　 2．实数与向量的积　　　3．向量共线定理

二、由平行四边形想到：

1．是不是每一个向量都可以分解成两个不共线向量？且分解是唯一？

2．对于平面上两个不共线向量，是不是平面上的所有向量都可以用它们来表示？

——提出课题：平面向量基本定理

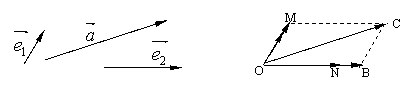三、新授：1．(P105-106)，是不共线向量，是平面内任一向量

=　　　　　 =λ₁　　  ==+=λ₁+λ₂

=　　　　　 =λ₂

得平面向量基本定理：如果，是同一平面内的两个不共线向量，那么对于这一平面内的任一向量，有且只有一对实数λ₁，λ₂使=λ₁+λ₂

注意几个问题：1°　、必须不共线，且它是这一平面内所有向量的一组基底

2° 这个定理也叫共面向量定理

3°λ₁，λ₂是被，，唯一确定的数量

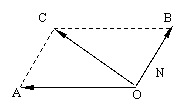
2．例一( P106例三)已知向量，　求作向量-2.5+3。

作法：1° 取点O，作=-2.5　 =3

　　　　　  2° 作　　 OACB，即为所求+

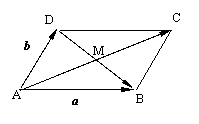
例二、(P106例4)如图　　 ABCD的两条对角线交于点M，且=，=，

用，表示，，和

　　　　　　　　　　　　　　　　　　　　　　　　　　　 解：在　　 ABCD中

　　　　　　　　　　　　　　　　　　　　　　　　　　　 ∵=+=+

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 =-=-

　　　　　　　　　　　　　　　　　　　　　　　　　　　 ∴=-=-(+)=--

==(-)=-　　　 ==+

=-=-=-+

例三、已知　　 ABCD的两条对角线AC与BD交于E，O是任意一点，

求证：+++=4

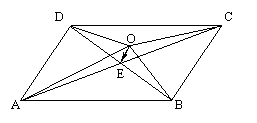　 证：∵E是对角线AC和BD的交点

　　　　∴==-

　　 　　 ==-

在△OAE中　　 +=

同理：+=　　　 +=　　　 +=

以上各式相加，得：+++=4

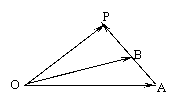
例四、(P107 例五)如图，，不共线，=t (tÎR)用,表示

　　　　  　　　　　　　　　　　　　　　　　　　　　　　解：∵=t

　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　∴=+=+ t

　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　 =+ t(-)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 =+ t-t

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  =(1-t) + t

四、小结：平面向量基本定理，其实质在于：同一平面内任一向量都可以表示为两个不共线向量的线性组合。

五、作业： 课本 P107 练习　 P108 习题5.3　 3-7