第十四教时
教材：平移
目的：要求学生理解“平移”的概念和平移的几何意义，并掌握平移公式，能运用公式解决有关具体问题。
过程：
一、平移的概念：点的位置、图形的位置改变，而形状、大小没有改变，从而导致函数的解析式也随着改变。这个过程称做图形的平移。（作图、讲解）
二、
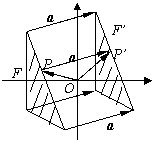平移公式的推导：
1．设P(x, y)是图形F上的任意一点，它在平移后的
图象F’上的对应点为P’(x’, y’)——
可以看出一个平移实质上是一个向量。
2．设
= (h, k)，即：
∴(x’, y’) = (x, y)
+ (h, k) ∴
—— 平移公式
3．注意：1°它反映了平移后的新坐标与原坐标间的关系
2°知二求一
3°这个公式是坐标系不动，点P(x, y)按向量a = (h, k)平移到点P’(x’, y’)。另一种平移是：点不动，把坐标系平移向量-a，即：
。这两种变换使点在坐标系中的相对位置是一样的，
这两个公式作用是一致的。
三、应用：
例一、（P121 例一）
1．把点A(-2, 1)按a = (3, 2)平移，求对应点A’的坐标(x’, y’)。
2．点M(8, -10)按a平移后对应点M’的坐标为(-7, 4)，求a。
解：1．由平移公式：
即对应点A’的坐标为(1, 3)
2．由平移公式：
即a的坐标为(-15, 14)
例二、将函数y = 2x的图象l按a = (0, 3)平移到l’，求l’的函数解析式。
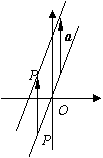解：设P(x, y)为l上任一点，它在l’上的对应点为P’(x’, y’)
由平移公式：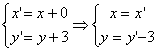
代入y = 2x得：y’ - 3 = 2x’ 即：y’ = 2x’ + 3
按习惯，将x’、y’写成x、y得l’的解析式：y = 2x + 3
（实际上是图象向上平移了3个单位）
例三、已知抛物线y = x2 + 4x + 7，
1．求抛物线顶点坐标。
2．求将这条抛物线平移到顶点与原点重合时的函数解析式。
解：1．设抛物线y = x2 + 4x + 7的顶点O’坐标为(h, k)
则h = -2, k = 3 ∴顶点O’坐标为(-2, 3)
3．按题设，这种平移是使点O’ (-2, 3)移到O(0, 0)，
设
= (m, n)
则
设P(x, y)是抛物线y = x2 + 4x + 7上任一点，对应点P’为(x’, y’)
则
代入y = x2
+ 4x + 7得：y’ = x’2
即：y = x2
四、小结：平移公式、应用
五、作业： P123 练习
P124 习题5.8