| 任意角的三角函数单元 一、选择题 1.若secθ·cscθ·tanθ<0,则θ属于( ) A.(2kπ-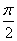 ,2kπ)(k∈Z) B.(2kπ+ ,2kπ)(k∈Z) B.(2kπ+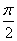 ,2kπ+π)(k∈Z) ,2kπ+π)(k∈Z) C.(2kπ+π,2kπ+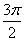 )(k∈Z) D. )(k∈Z) D.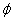 2.已知x∈[0,2π],集合M={x|sinx>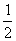 },N={x|cosx< },N={x|cosx<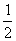 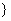 .则M∩N=( ) .则M∩N=( ) A.{x|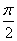 <x< <x<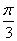 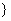 B.{x| B.{x|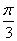 <x< <x<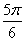 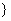 C.{x|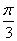 <x< <x<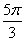 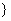 D.{x| D.{x|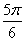 <x< <x<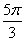 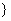 3.函数y=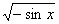 + +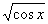 的定义域为( ) 的定义域为( ) A.[2kπ,2kπ+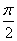 ],k∈Z B.[2kπ+ ],k∈Z B.[2kπ+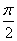 ,2kπ+π],k∈Z ,2kπ+π],k∈Z C.[2kπ+π,2kπ+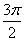 ],k∈Z D.[2kπ- ],k∈Z D.[2kπ-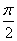 ,2kπ],k∈Z ,2kπ],k∈Z 4.cos(kπ-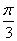 )(k∈Z)的值是( ) )(k∈Z)的值是( ) A. 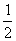 B.± B.±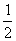 C.- C.- 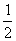 D.(-1)k D.(-1)k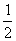 5.函数f(x)=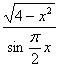 的定义域是( ) 的定义域是( ) A.[-2,2] B.(-2,2) C.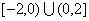 D.(-2,0)∪(0,2) D.(-2,0)∪(0,2) 6.若α=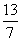 π 则( ) π 则( ) A.sinα>0且cosα>0 B.sinα>0且cosα<0 C.sinα<0且cosα<0 D.sinα<0且cosα>0 7.在△ABC的内角A满足sinA+cosA>0且tanA-sinA<0,则A的取值范围是( ) A.(0,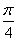 ) B.( ) B.( 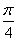 , ,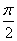 ) C.( ) C.( 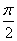 , ,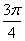 ) D.( ) D.( 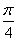 , ,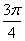 ) ) 8.设α,β∈(0,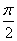 ),则下列式子成立的是( ) ),则下列式子成立的是( ) A.sin(α+β)<α+β<sinα+sinβ B.sin(α+β)<sinaα+sinβ<α+β C.sinα+sinβ<sin(α+β)<α+β D.sinα+sinβ<α+β<sin(α+β) 9.sinθ+cosθ=2sinA,sinθcosθ=sin2B,则下列各式中正确的是( ) (参考公式sin2θ=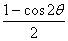 ) ) A.cos2A=cos2B B.2cos2A=cos2B C.cos2A=2cos2B D.cos2A=2cosB 10.设f(x)=(sinα)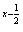 ,若f(log2sinα)= ,若f(log2sinα)=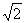 且0<α< 且0<α<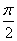 ,则α的值是( ) ,则α的值是( ) A. 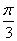 B. B. 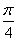 C. C. 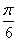 D. D. 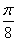 二、填空题 11.若函数f(x)=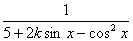 的值恒为E,则k的取值范围为 . 的值恒为E,则k的取值范围为 . 12.设θ∈(0,2π),若P(sinθ,cos2θ)点在第三象限,则θ的取值范围是 . 13.若f(tanx)=|sinx|,则f(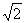 )= . )= . 14.已知f(n)=sin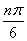 (n∈N),则f(1)+f(2)+…+f(2002)的值等于 . (n∈N),则f(1)+f(2)+…+f(2002)的值等于 . 三、解答题 15.若对任意x∈R,不等式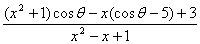 >sinθ-1恒成立,求θ的取值范围. >sinθ-1恒成立,求θ的取值范围. 16.已在函数f(x)=2msinx-2cos2x+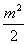 -4m+3,m∈(-∞,-2]最小值为19,求函数f(x)的最大值及取得最大值时的x的值. -4m+3,m∈(-∞,-2]最小值为19,求函数f(x)的最大值及取得最大值时的x的值. 17.已知角α的终边经过点P(8t,15t)(t≠0),求log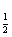 |secα-tanα|的值. |secα-tanα|的值. 18.若sinx=2cosx,求sin2x+sinxcosx+3cos2x的值. 【能力素质提高】 1.求函数y=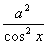 + +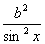 (a>b>0,0<x< (a>b>0,0<x<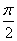 )的最大值与最小值. )的最大值与最小值. 2.若{x|cos2x+sinx+m=0}≠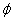 ,求m的取值范围. ,求m的取值范围. 3.已知sinx+cosx=sinxcosx,求sin3x+cos3x的值. 【综合实践创新】 1.把函数f(x)=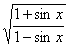 表示成一个奇函数g1(x)与一个偶函数g2(x)之和,求g1(x)·g2(x)及g12(x)-g22(x)的值. 表示成一个奇函数g1(x)与一个偶函数g2(x)之和,求g1(x)·g2(x)及g12(x)-g22(x)的值. 2.已知sinθ=asinφ,tanθ=btanφ(θ为锐角),用a、b来表示cosθ. 3.在矩形ABCD中,P为对角线BD上一点,AP⊥BD,PE⊥BC,PF⊥CD, 求值:(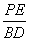 ) )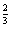 +( +(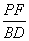 ) ) 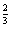 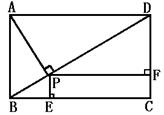
参考答案 【课内四基达标】 一、1.D 2.B 3.D 4.D 5.D 6.D 7.C 8.B 9.B 10.B 二、11.-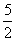 <k< <k<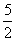 12.( 12.( 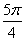 , ,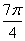 ) 13. ) 13. 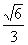 14. 14. 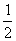 三、15.解:原不等式变形为:(cosθ-sinθ+1)x2-(cosθ-sinθ-4)x+cosθ-sinθ+4>0 令t=cosθ-sinθ得:(t+1)x2-(t-4)x+t+4>0 ∴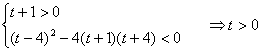 ∴cosθ-sinθ>0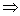 cosθ>sinθ cosθ>sinθ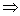 2kπ- 2kπ-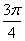 <θ<2kπ+ <θ<2kπ+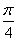 k∈Z k∈Z 16.解:f(x)=2sin2x+2msinx+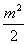 -4m+1 -4m+1 当sinx=1时 f(x)min=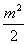 -2m+3=19 -2m+3=19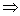 m=-4 或8(舍去) m=-4 或8(舍去) ∴f(x)=2sin2-8sinx+25 当sinx=-1时 即x=2kπ-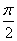 (k∈Z)时 f(x)max=35 (k∈Z)时 f(x)max=35 17.解:当t>0时 ∴r=17t secα=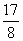 tanα= tanα=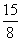 ∴原式=log ∴原式=log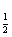 | |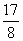 - -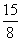 |=2 |=2 当t<0时 ∵r=-17t secα=-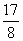 tanα= tanα=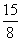 ∴原式=log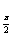 |- |-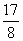 - - 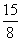 |=-2 |=-2 18.解:∵tanx=2 ∴原式=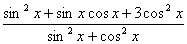 = =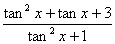 = =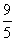 【能力素质提高】 1.解:∵y=a2sec2x+b2csc2x=a2+b2+a2tan2x+b2cot2x=(a2+b2+2ab)+(atanx-bcotx)2 =(a+b)2+(atanx-bcotx)2≥(a+b)2 ∴y无最大值.ymin=(a+b)2 2.解:∵m=sin2x-sinx-1 ∴m∈[-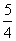 ,1] ,1] 3.解:令t=sinx+cosx ∴sinx+cosx=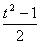 t∈[- t∈[-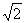 , ,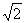 ] ] ∴t=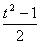 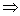 t=1- t=1-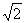 ∴原式=(sinx+cosx)(sin2x-sinxcosx+cos2x)=t(1-t)=(1-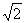 )× )×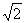 = =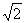 -2 -2 【综合实践创新】 1.解:∵g1(x)=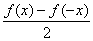 g2(x)= g2(x)=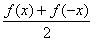 ∴g1(x)·g2(x)=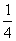 [f2(x)-f2(-x)]= [f2(x)-f2(-x)]=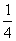 ( (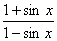 - -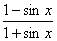 )= )=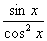 2.解:∵sinφ=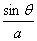 tanφ= tanφ=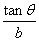 ∴cosφ=acscθ cotφ=bcotθ ∴cosφ=acscθ cotφ=bcotθ ∴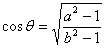 ,b≠±1 ,b≠±1 3.令∠DBC=α.则∠DPF=∠BDA=∠BAP=α ∴PE=BPsinα=ABsin2α=BDsin3α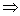 ( (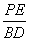 ) )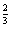 =sin2α =sin2α PF=DPcosα=ADcos2α=BDcos3α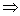 ( (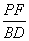 ) ) 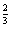 =cos2α =cos2α ∴原式=sin2α+cos2α=1 |