三角函数

期末数学复习提纲（一）——三角函数

一、基本概念、定义：

1. 角的概念推广后，包括　　　、　　　、　　　，与α终边相同的角表示为　　　　　　　  。

　终边角： x轴上　　　　　　　　　　　　  　y轴上　　　　　　　　　　　　　　  　

　　　　　 第一象限　　　　　　　　　　　   第二象限 　　　　　　　　　　　　　　  

　　　　　 第二四象限　　　　　　　　　　   直线y＝x上　　　　　　　　　　　　  　

2. 弧度制：把　　　　　　　　　　　　　　　　　 叫1弧度的角。

　公式：α＝—　　　　  换算：180°＝　　　 弧度； 1弧度＝　　 度； 1°＝　　 弧度
　扇形： 弧长L＝　　　 ＝　　　　　 ，面积S＝　　　　　 ＝

3. 任意角的三角函数：

①定义：角α终边上任意一点P(x，y)，则r＝ 　　　　　 ，六个三角函数的定义依次是　　　　  、

　　　　　  、　　　　　  、　　　　　  、　　　　　  、　　　　　  。

②三角函数线：角的终边与单位圆交于点P，过点P作　　 轴的垂线，垂足为M，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　 。过点A(1,0)作　　　　  ，交　　　　　　　　　于点T，则　　　　　   。

③同角三角函数关系式：

 平方关系：　　　　　 商数关系：　　　　  倒数关系：　　　　　　　　

④诱导公式：

角x	Sinx	Cosx	Tanx	Sin(－α)＝　　　　　  cos(－α)＝　 　 Tan(－α)＝　 　 能推导：＋α；＋α；－α 　 口诀：函数名变反，符号看象限。
π—α
π＋α
—α
2π-α
2kπ+α
口诀

二、基本三角公式：（1～2要求能熟练运用：顺用、逆用、变形用，3～6要求能证明，不记忆）

1．和、差角公式

　　　　　  　　　　　　　　　 

2．二倍角公式

　　　　　　 　　　　　 ＝　　　　  ＝　　　　　　　

倍角公式变形：降幂公式

　　　　　  　　　　　　　　

3．半角公式(书P45～46)

,　,　

4．万能公式：　 ；；．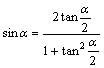

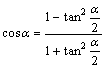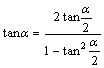5．积化和差公式(书P46～47)

；　　；

；　 ．

6．和差化积公式(书P46～47)

；　　　 ；

；　　  ．

应用公式解题的基本题型：化简、求值、证明

基本技巧：

①1的妙用：1＝　　　　　  ＝　　　　  ＝

②变角： (x+y)＋(x－y)＝　　 (x+y)＋(x－y)＝　　　 α＝　　　＝　　　　  ＝　　　　　 等

③变名：切化弦；弦化切

④化一：a sinx＋b cosx＝　　　　 

 

三、三角函数性质

函数	正弦函数y＝sinx	余弦函数y=cosx	正切函数y＝tanx
图像
定义域
值域	值域： 当x＝　　　　  时y最小； 当x＝　　　　  时y最大；	值域： 当x＝　　　　  时y最小； 当x＝　　　　  时y最大；	值域：
周期/奇偶	周期T＝　　 奇偶性：	周期T＝　　 奇偶性：	周期T＝　　 奇偶性：
单调性	增： 减：	增： 减：	增区间：
对称中心
对称轴

四、y＝Asin(ωx＋ψ)的图像和性质：

1、　作图：五点法，依次取ωx＋ψ＝

2、　周期T＝　　　

3、　单调区间：Aω>0时，增区间：解不等式　　　　 ≤ωx＋ψ≤

　　　　　　　　　　 　　减区间：解不等式　　　　 ≤ωx＋ψ≤

Aω<0时，增区间：解不等式　　　　 ≤ωx＋ψ≤

　　　　　　　　　　　　 减区间：解不等式　　　　 ≤ωx＋ψ≤

4、最大值：A>0时，当ωx＋ψ＝　　　　　　　  时，y取最大值A。

 最小值：A>0时，当ωx＋ψ＝　　　　　　　  时，y取最小值－A。

5、概念：振幅　　　；周期T＝　　　 ；频率f＝　　　　 ；初相　　　　　  ；相位　　　　。

6、三角变换： (A>0，ω>0)

　将y＝sinx的图像—————————>y＝sin(x＋ψ) ——————————>y＝sin(ωx＋ψ)

——————————>y＝Asin(ωx＋ψ)

或者：　将y＝sinx的图像—————————>y＝sin(ωx) —————————>y＝sin(ωx＋ψ)

——————————>y＝Asin(ωx＋ψ)

7、联系： y＝tan((ωx＋ψ)　(ω>0)的周期是T＝　　　 ，单调　 区间是解不等式　　　　　　  。

五、反三角定义：

1.在闭区间　　　　 上，符合条件sinx＝a (-1≤a≤1)的角x叫a的反正弦，记作：x＝

在闭区间　　　　 上，符合条件cosx＝a (-1≤a≤1)的角x叫a的反余弦，记作：x＝

在开区间　　　　 上，符合条件tanx＝a的角x叫a的反正切，记作：x＝

2.反三角的三角函数、三角函数的反三角：

例：sin(arcsinx)＝　　　 ，其中x∈[-1,1]；arcsin（sinx）＝　　　 ，其中x∈[－，]；

六、数学思想方法：  数形结合思想，例如：解三角不等式可以用　　　　  、或　　　　　  ；

整体思想，例如：研究函数y＝Asin(ωx＋ψ)的图像和性质可以把 　　　　　　 看成整体

2007届期末数学复习提纲（二）——平面向量

一、向量知识：

（1）　　　　　　　　　　　　　　　 叫做向量。

（2）向量的运算：

运算	定义 或 法则	运算性质（运算律）	坐标运算
加　法
减　法
实数与向量的积
数量积	几何意义：

（3）平面向量的基本定理：

如果和是同一平面内的两个不共线的向量，那么　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　  　　 。

（4）两个向量平行和垂直的充要条件：

　　　　　　　　　　  　　　　　　　　　；

∥　　　　　　　　　　 　　　　　　　　　；

（5）夹角、模、距离等计算：

夹角：与的夹角

模： ＋＝　　　　　　　　　　  －＝　　

＋＋＝

模＝　　　　　　  两点距离公式：PP＝　　　　　　　　　　　  向量=

计算：求与＝(a，b)共线的单位向量

（6）线段的定比分点坐标公式：

设，且，则

时，得中点坐标公式：　　　　　 可推出三角形重心坐标公式：

（7）平移公式

点按平移到，则

点　　　　点P(a,b) 点　　　　

曲线y＝　　　　　  曲线y＝f(x) 曲线y＝　　　　

二、解斜三角形

（1）正弦定理：　　　 =　　　　  =　　　

（2）余弦定理：　　　　　　　　　　　　 

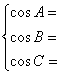
（3）S＝　　　　　　　 ＝　　　　　　　 ＝　　　　　　　　

（4）解三角形的几种类型及步骤：

①已知两角一边： 先用　　　　　　　　　　 →再用　　　　　　　　　　　　　　　　　  。

②已知两边及夹角：先用　　　　　　　　　　→再用　　　　　　　　　　　　　　　　　  。

③已知两边及一边对角：先用　　　　　　　　　　　　　　 （注意：解；内角和）

→再用　　　　　　　　　　　　  　　　　　　　　　　　　　　　　　　 。

④已知三边：先用　　　　　　　　　　　　　 →再用　　　　　　　　　　　　　　　　  。

（5）解应用问题的一般步骤：①　　　　→ ②　　　　 → ③　　　　 → ④

2007届期末数学复习提纲（三）——不等式

一、不等式的性质

1、　定理1：

2、　定理2：

3、　定理3：

推论：

4、　定理4：

推论1：

推论2

5、定理：

二、算术平均数与几何平均数

定理：如果，那么，当且仅当时取“=”号。

推广1：（四个平均数）

推广2：（3个数）如果，那么

最值结论（书例1）：

三、不等式的证明方法：

1、　比较法：（作差或作商）最基本、最重要的方法。

步骤：作差（商）—变形—判断符号

2、　综合法：

3、　分析法：

4、　构造函数，利用函数单调性：

5、　放缩法：

四、不等式的求解

五、含有绝对值的不等式

 2007届期末数学复习练习（一）——三角函数

一、选择题

1、　tan70°＋tan50°－tan70°tan50°的值是　　　。

A.　　　　　　　　 B.　　　　　　　C.－　　　　　　D.－

2、　在直角三角形中两锐角为A和B，则sinAsinB　　　。

A.有最大值和最小值0 B.有最大值，但无最小值
C.既无最大值也无最小值　　　　　　　　　 D.有最大值1，但无最小值

3、　已知sinα＝，并且α是第二象限的角，那么tanα的值等于　　  。(91(1)3分)
A.－　　　　　　B.－　　　　　　 C.　　　　　　　 D.

4、　函数y＝sin(2x＋)的一条对称轴的方程是　　　。(91(5)3分)
A.x＝－　　　　 B.x＝－　　　　　C.x＝　　　　　　D.x＝

5、　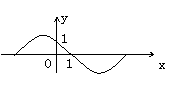如果右图是周期为2π的三角函数y＝f(x)的图像，那么f(x)可以写成　　  。(91三南)
A.sin(1＋x)　　　　B.sin(－1－x)
C.sin(x－1)　　　　D.sin(1－x)

6、　已知集合E＝{θcosθ＜sinθ，0≤θ≤2π}，F＝{θtgθ＜sinθ}，那么E∩F为区间　　　。(93(11)3分)

A.(，π)　　　　B.()　　　　 C.(π，)　　　　 D.()

7、　设θ是第二象限的角，则必有　　　。(94(4)4分)
A.tan

8、　函数y＝4sin(3x＋)＋3cos(3x＋)的最小正周期是　　　。(95(3)4分)
A.6π　　　　　　　B.2π　　　　　　　C.　　　　　　　D.

9、　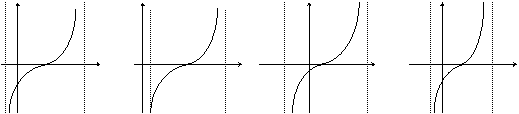函数y＝tan()在一个周期内的图象是　　　。(97(3)4分)

A. y　　　　　　　　　 B. y　　　　　　　C.　　　y　　　　　D.　 　 y


－ o　 　　　 x　 o 　　　 　x 　－ 　 o　　 　x　 －　 o　　　x

10、已知点P(sinα－cosα，tanα)在第一象限，则在[0，2π]内α得取值范围是　　　。
A.()　　　　　　　　　　　　B.()
C.()　　　　　　　　　　　D.(，π)

11、函数f(x)＝Msin(ωx＋φ)(ω＞0)在区间[a，b]上是增函数，且f(a)＝－M，f(b)＝M，则函数g(x)＝Mcos(ωx＋φ)区间[a，b]上　　　。

A.是增函数B.是减函数　C.可以取得最大值M　　D.可以取得最小值－M

12、设α，β是一个钝角三角形的两个锐角，下列四个不等式中不正确的是　　　。A.tanαtanβ＜1　　　B.sinα＋sinβ＜
C.cosα＋cosβ＞1　　　　　　　　　　　　D.tan(α＋β)＜tan

二、填空题

1. 关于函数f(x)＝4sin(2x＋)(x∈R)，有下列命题:
①由f(x₁)＝f(x₂)＝0可得x₁－x₂必是π的整数倍；
②y＝f(x)的表达式可以改写成y＝4cos(2x－)；
③y＝f(x)的图像关于点(－，0)对称；
④y＝f(x)的图像关于直线x＝－对称.
其中正确的命题序号是_________.(注:把你认为正确的命题序号都填上)

2. 函数y＝sinxcosx＋sinx＋cosx的最大值是___________.

3. 函数y＝sin(x－)cosx的最小值是___________.

4.　　 的值为______________.

5. 函数f(x)＝3sinxcosx－4cos²x的最大值是___________。

三、解答题

1、已知定义在R上的函数周期为

（1）写出f(x)的表达式；

（2）写出函数f(x)的单调递增区间；

（3）说明f(x)的图象如何由函数y=2sinx的图象经过变换得到.

2、　已知A、B、C的坐标分别为A（3，0），B（0，3），C（），

　　　 （I）若求角的值；

　　　 （II）若的值.

3、求函数）的最小值，并求其单调区间.

4、已知锐角△ABC中，三个内角为A、B、C，两向量，是共线向量。

（I）求∠A的大小；（II）求函数y=2sin²B+cos()取最大值时，∠B的大小。

5、已知函数、b为常数，且）的图象过点（），且函数的最大值为2.

（1）求函数的解析式，并写出其单调递增区间；

（2）若函数的图象按向量作移动距离最小的平移后，使所得的图象关于y轴对称，求出向量的坐标及平移后的图象对应的函数解析式.

6、设最高点M（2，），由最高点运动到相邻的最低点N时，曲线与x轴交于K（6，0）.

　　　 （I）求A、、的值；（II）求满足的所有x值的集合.

7、 已知定义在区间上的函数的图象关于直线对称，

当时，函数，其图象如图所示.

(1) 求函数在的表达式；

(2) 求方程的解.

8、已知函数

（1）设>0为常数，若上是增函数，求的取值范围；

（2）设集合若A  B，求实数m的取值范围.

9、已知函数

（1）　　　 试求函数的值域；（2） 讨论的奇偶性；（3） 画出的图象

 2007届期末数学复习练习（二）——平面向量

§5.1　 向量的概念、向量的加法、减法、实数与向量的积

【复习目标】1、理解有关向量的概念，掌握向量加减法作图。2、掌握实数与向量的运算法则及运算律，理解两个向量共线的充要条件3、了解平面向量基本定理，理解平面向量的坐标的概念，掌握平面向量的坐标运算。4、培养学生的观察、分析、归纳、抽象的思维能力。

【基础训练】

1、两向量共线是两向量相等的_______

A　充分不必要条件　B　必要不充分条件　C 充要条件  D　既不充分也不必要条件

2、当且不共线时，与的关系是______

A　平行　B  垂直　C  相交但不垂直　D  相等

3、给出以下四个命题：(1)若两非零向量，使得，那么；(2)若两非零向量，则；(3)若，则；(4)若，则与共线。其中正确命题的个数是_____

A　1  B　 2　 C　3  D　4

4、向量与共线且方向相同，则=_______

5、设平行四边形ABCD的对角线交于O，交，则=________

【例题】

1、设不共线，已知，，。若三点共线，求实数的值。

2、若非零向量满足，求与所成角的大小。

3、已知,且，求M,N的坐标和

4、已知向量且，求

6、　在的边上分别取，使，，设线段于的交点为，，。用表示

§5.2　向量的数量积

【复习目标】1、掌握平面向量的数量积及其几何意义，了解平面向量数量积可以处理有关长度、角度和垂直的问题，掌握向量垂直的充要条件。2、培养学生的化归思想、数形结合思想和分析问题、解决问题的能力。

【基础训练】1、对于任意向量,与的大小关系是______

A  <  B  >  C  　D  无法确定

2、已知，且与垂直，则与的夹角为_______

A　60°　B  90°　C  45°　D  30°

3、设是任意的非零平面向量，且相互不共线，则(1)

(2)　　(3)不与垂直

(4)中，是真命题的有____

A　(1)(2)　B  (2)(3)　C　(3)4)　D  (2)4)

4、已知且起点为(1,2)，终点为，则=____

5、已知，且与的夹角为钝角，则的取值范围是______

A  B  C  D　

6、设是所在平面内一点，且，则是的（ ）

A、内心　　　　B、垂心　　　　 C、外心　　　　　　　 D、重心

7、求与

【例题】

1、判断下列各命题正确与否；(1)若，则；(2)若，则当且仅当时成立；(3)对任意向量都成立；(4)对任一向量，有

2、三角形ABC中，A(－5,1)，B(－1,7)，C(1,2)，求BC边上的中线AM的长。(2)∠CAB的平分线AD的长。(3)cos∠ABC的值。

3、已知点A(1,2)和B(4，－1)，问能否在轴上找到一点C，使∠ACB=90°，若不能，说明理由，若能，求出C点坐标。

4、设，试求满足的的坐标(O为原点)

5、设与是非零向量，且，，求与夹角。

6、已知，，满足关系；

（1）用表示；　（2）求的最小值，和此时的两个向量之间的夹角。

7、已知向量，，1求的夹角2若与垂直，求

8、已知是内部一点，，，设，，，且，用表示

9、已知的顶点为，边上的高为，求

10、已知向量，且，

（1）　　　 若，求值；（2） 的最小值是，求

§5.3　 两点间的距离公式、线段的定比分点与图形的平移

【复习目标】1、掌握两点间的距离公式及线段的定比分点和中点坐标公式，并能熟练应用。2、掌握平移公式。3、培养学生用化归思想解决问题的能力。

【基础训练】1、已知A(－1,1)，B(3,5)，点P分有向线段所成的比为，则点P的坐标为____

A　(7,－9)　　　B　(－7,9)　　 C　(7,9)　　　D　(－7，－9)

2、把函数的图象F按，平移到F^/，则F^/的函数式为____

A 　　 B 　　C 　　D　

3、设A、B、C三点共线，且它们的纵坐标分别为2,5,10，则A点分所得的比为_____

A 　　　　　 B 　　　　　 C 　　　　　 D　－

4、已知，C为上距A较近的一个三等分点，D为上距C较近的一个三等分点，则用表示的表达式为_____

A　　　　　　 B 　　　　C 　　　　　D　

5、向量满足，则的最大值和最小值是______

6、若点P分所成的比是，则点A分所成的比是____

7、把一个函数的图象左移个单位，再向下平移2个单位得到的解析式为：，则原函数的解析式为_______

【例题】1、已知点A，B(5,2)，线段AB上的三等分点依次为，求点的坐标以及A、B分所成的比。

2、函数的图象按向量平移后，图象的解析式为，求向量。

§5.4　　解斜三角形

【复习目标】掌握正弦定理、余弦定理，并能初步运用它们及有关的三角知识解三角形及有关的实际应用问题；培养学生的化归思想和分析问题、解决问题的能力。

【基础训练】1、在中，如果，则A等于_____

A　150°　B  120°　C　 60°  D　30°

2、已知中，则B等于_____

A　60°　B  120°　C  30°　D  60°或120°

3、在中，若，则是_____

A　等腰三角形　B  直角三角形　C  等边三角形　D  等腰直角三角形

4、中，若，则的形状是______

5、中，已知，且，则sinC等于_____

6、在中，若，则A=_______

7、在中，若则=_______

【例题】1、已知是中∠A、∠B、∠C的对边，S是的面积，若

，求的长度。

2、在中，已知，求A、C及边。

3、在中，A、B、C成等差数列，求证：

4、在中，角A、B、C对边分别为，证明：.

5、如图：有两条相交成60°角的直路，交点是O，甲、乙分别在上，起初甲离O点3，乙离O点1，后来两人同时用每小时4的速度，甲沿的方向，乙沿的方向步行。(1)起初两人的距离是多少？(2)用包含的式子表示小时后两人的距离。(3)什么时候两人的距离最短？

平面向量单元测试题

一、选择题：

1、　在四边形ABCD中，设，则=_____

A 　　　B 　　　C 　　 D　

2、　与平行的单位向量为______

A　　 B  　 C  或　  D　

3、　已知中，则=____

A　　　　 B － 　　　C  　　　　　D　－

4、　非零向量是的_____

A　充分而不必要条件　B　必要不充分条件　C　充要条件　D  既不充分也不必要条件

5、　　已知两点，则点分有向线段所成的比和值分别为

A　和　　　 B　和8　　　　 C　和4　　　　  D　和

6、设分别是平面直角坐标系内轴和轴正方向上的两个单位向量，已知

，则四边形ABCD的面积是____

A　20　　　　　  B　30　　　　　  C 　　　　 D　45

7、设A(1,2)，B(3,－1)，C(3,4)，则=____

A　 11　　　  B　 5　　　  C　－2　　　  D　1

8、将函数按平移使其化简为反比例函数表达式，则=____

A　　　　B 　　　 C 　　　 D　

9、在中，角A、B、C的对边为，若，则角C等于

A　30°　　　 B　45°　　　 C　 60°　　　D　120°

10、已知，，且恰有，则A、B、C三点_____

A　 构成直角三角形　　 B　构成等腰三角形　　 C　共线　　　D　无法确定

11、在中，已知，若利用正弦定理解有两解，则的取值范围是______　

 A 　　 B 　　　C 　　　　D　

12、已知中，若，则是_____

A　等腰三角形　　 B　直角三角形　　　C　等腰直角三角形　　 D　等腰或直角三角形

二、填空题：

13、已知：A(2,3)，B(1,4)且，则=______

14、已知，且与为不共线的非零向量，则的面积可表示为_____

15、已知的BC边长的中点M，则=_____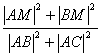

16、运用物理中矢量运算及向量坐标表示与运算，我们知道：(1)若两点等分单位圆时有相应关系式为：(2)四点等分单位圆时有相应关系式为：
，由此可以推知三等分单位圆时的相应关系式为_______

三、解答题：

17、已知是两个不共线非零向量，若

(1)　　求证：A、B、D三点共线；(2)确定实数的值，使与共线。

18、设A、B为单位圆上两点，O为坐标原点，(A、O、B不共线)(1)求证：与垂直；(2)当且时，求的正弦值。

19、海中有岛A，已知A岛四周8海里内有暗礁，今有一货轮由西向东航行，在B处望见A岛在北偏东75°，行海里至C后见此岛在北偏东30°，如货轮不改变航向继续航行，问有无触礁危险？

20、已知,且 (1)求与的关系；(2)证明.

21、在一很大的湖岸边（可视湖岸为直线）停放着一只小船，由于缆绳突然断开，小船被风刮跑，其方向与湖岸成15°角，速度为2.5km/h，同时岸边有一人，从同一地点开始追赶小船，已知他在岸上跑的速度为4km/h，在水中游的速度为2km/h.

问此人能否追上小船.若小船速度改变，则小船能被人追上的最大速度是多少？

22、设平面向量，若存在不同时为0的两个实数，及实数，使且，(1)求函数关系式；(2)若在是单调函数，求证：。

2007届期末数学复习练习（三）——不等式

高二数学第六章不等式单元练习一

一．选择题

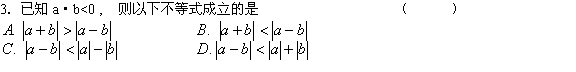
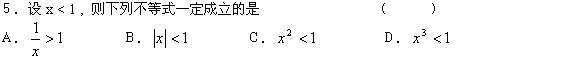
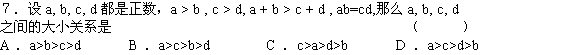
二．解答题

高二数学第六章不等式单元练习二

一．　　　　　　 选择题：

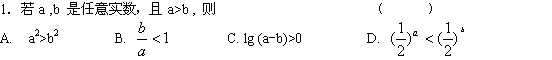
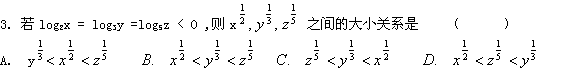
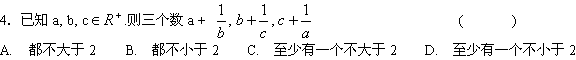
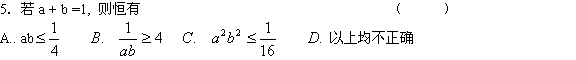
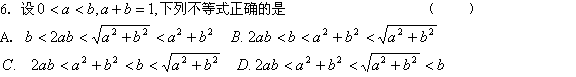
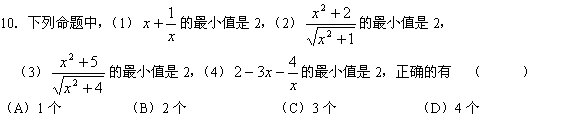
二．解答题：

高二数学第六章不等式单元练习三　

一．选择题：

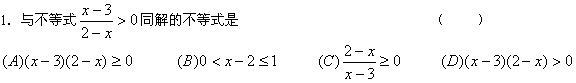
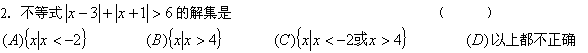
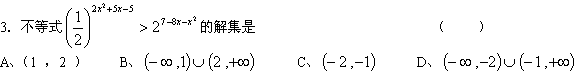
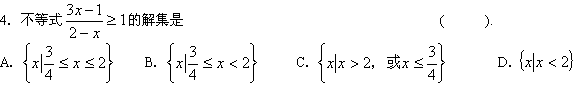
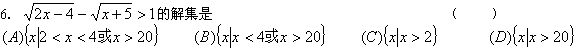
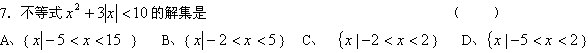
二．解答题：