高一下学期数学期中考试试卷
时量:120分钟 总分:150分 命题人:龚光元
一、选择题（共12小题，每小题5分，总计60分，每小题只有一个正确答案，请将正确答案填写在后面的答题卷上。）
1、已知集合
＝
，则集合的元素的个数为（ ）
(A) 10 (B) 9 (C) 8 (D) 7
2、若
＝
，
，则正确的是（ ）
(A) 
(B)
(C) ＝ (D) Ë
3、设
＝{1，2，3，4，5}， ＝{2，4，5}， ＝{1，3，4}，那么（
）∩（
）等于（ ）
(A)
(B) {4}
(C) {1，3} (D)
{2，5}
4、已知方程
的两根为
，
且＜，若
＜0，则不等式
的解为（ ）
(A)一切实数 (B) 
(C) 
或
(D) 无解
5、若函数
的定义域为
，则
的范围为（
）
(A) ［1，19］ (B) ［1，19） (C)（1，19） (D)（1，19］
6、“
”为真，“
”为假，“
”为真的是（ ）
(A)
:23为偶数，
：32是奇数 (B) :1＋3＝5，：3＞1
(C):a∈{a，b}，：{a}{a，b} (D):
，：
7、函数
的图象大致是（
）
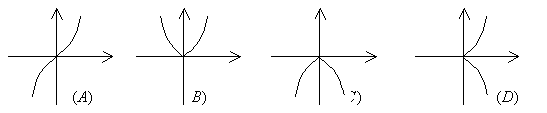
8、命题“若m≥0，则x2＋x－m＝0有实根”的逆否命题为( )
(A) 若x2＋x－m＝0有实根，则m≥0。
(B) 若m≤0，则x2＋x－m＝0没有实根。
(C) 若x2＋x－m＝0没有实根，则m＜0。
(D) 若m＜0，则x2＋x－m＝0没有实根。
9、下列命题为真命题的是（ ）
(A)“
”是“
”的充要条件；
(B)“A∩B≠”是“”的必要不充分条件；
(C)“x∈N”是“x∈R”的必要不充分条件；
(D)“p是q的充分条件”是“q是p的必要条件”的充要条件。
10、已知函数
＝－
(χ≥1),则它的反函数是 （ ）
(A)
+1 
∈R)
(B) y ＝
+1 (χ>0)
(C) y ＝
+1 (
≤0) (D) y ＝
(
≤0)
11、若
，则
为（ ）
(A)10 (B) 11 (C) 12 (D) 13
12、函数
的增区间为（ ）
(A)（－∞，－7］ (B)［－15，－7］
(C)［－7，1］ (D)
二、填空题（共4小题，每小题4分，总计16分，请将正确答案填写在后面的答题卷上。）
13、计算
=
。
14、函数y = x－
的值域为___________。
15、50名学生参加跳远和铅球两项测试，跳远和铅球两项及格的分别为40人和35人，两项均不及格的是4人，则两项测试都及格的人数为___________。
16、一般地，对于定义域为I的函数
,如果对于I内的任一，都有
，那么我们就说函数为偶函数。分析下列命题：
①
是偶函数；②
，
(－2，3)是偶函数；③偶函数的图象关于
轴对称；④偶函数的的图象关于轴对称。
其中正确命题的序号为___________。
下学期高一期中考试
数学答题卷
一、选择题答案(每小题5分,共计60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题答案(每小题4分,共计16分)
13 14 15 16
三、解答题(共6大题，共计74分)
17、（本大题满分10分）根据已有的证据，可以得到如下三个判断：①如果A无罪，则B与C都有罪；②在B与C中必有一人无罪；③要么A无罪，要么B有罪。
⒈用A、B、C分别表示“A有罪”、“B有罪”、“C有罪”，（本小问共4分）
⑴用逻辑联结词表述出判断①为 (本空2分)
⑵判断下列命题的真假：Ⅰ、
或
(
) ,Ⅱ、
或B ( )。
⒉试推断：A，B，C中究竟谁无罪？（本小问6分,要有详细的推导过程。）
18、（本大题满分12分）已知函数
，用定义证明：在
上是增函数。
19、（本题满分12分）某公司每月生产一种产品的固定成本为20000元，每生产一个产品增加投入100元，已知总收益满足函数：
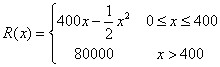（其中x是产品的月产量），求每月生产多少产品时公司的利润最大？最大利润是多少？（总收益＝总成本＋利润）
20、（本题满分13分）已知函数
在区间［0,1］上的最大值为2，求实数的值。
21、（本题满分13分）设集合A = ｛
｝， B = ｛x 
｝，C = ｛
｝，如果 (A∩B)
C，求实数m的取值范围。
22、（本题满分14分）已知的定义域为（0，＋∞），在（0，＋∞）上为增函数，对于任意的
（0，＋∞）都有
，且
＝1 。
①求
的值；（本小问4分）
②解不等式
。（本小问10分）
下学期高一期中考试
数学答题卷
一、选择题答案(每小题5分,共计60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | A | C | B | B | A | C | D | C | B | B |
二、填空题答案(每小题4分,共计16分)
13、 
14、(－
，
］ 15、 29 16、①③
三、解答题(共6大题，共计74分)
17、⒈（本小问共4分）
⑴①为 
(本空2分)
⑵Ⅰ、或 ( 真 ) ,（1分） Ⅱ、或B ( 真 )（1分）
⒉（本小问6分）
①的逆否命题为：
，结合②可知：为真 ¼¼¼¼¼¼¼¼¼¼ 2分
结合③知为真 ¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼
3分
从而结合②为真，即
为假 ¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼ 5分
故、都有罪，无罪。¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼ 6分
18、证明:任取
，则有
＝
－
¼¼¼ 3分
＝(
)－(
)＝(
)＋(
)
＝()＋
＝()
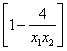¼¼¼¼ 7分
又∵，∴
且
，∴
∴
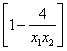，∴() ＜0
¼¼¼¼ 10分
故有
，即
¼¼¼¼11分
所以函数在上是增函数。
¼¼¼¼12分
19、解:设月产量x个，总利润为，则月总成本为20000＋100x，且有：
＝
－（20000＋100x）
¼¼¼¼¼ 2分
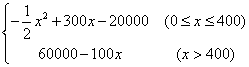¼¼¼¼¼ 5分
当
时，
＝
，所以当
时，
＝25000
¼¼¼¼¼ 8分
当
时，
是减函数，
所以＜60000－100×400＝25000。
¼¼¼¼¼ 10分
综上所述，当时，＝25000。
¼¼¼¼¼ 11分
∴每月生产300个时利润最大，最大利润为25000元。 ¼¼¼¼¼ 12分
20、解：
，故其图像是开口向下的抛物线，其对称轴是
，所以函数在（－∞，
］上是增函数，在［，＋∞）上是减函数。
¼¼¼¼¼ 3分
所以①当
，即
时，的最大值为
＝2，
或
。而此两个取值均不符合要求，故舍去。
¼¼¼¼¼ 6分
②当
，即
时，在［0,1］上是减函数，
故
＝
＝
＝2 
，满足条件。 ¼¼¼¼¼ 9分
③当
，即
时，在［0,1］上是增函数，
故＝
＝
＝2 
，亦满足条件。 ¼¼¼¼¼ 12分
综上所述，或。
¼¼¼¼¼ 13分
21、解：由
，
∴＝（－3，5）
¼¼¼¼¼ 2分
又由（以下即可以分内讨论，亦可以数形结合）
，∴＝（4，＋∞）
¼¼¼¼¼ 5分
A∩B＝（4，5）。
¼¼¼¼¼ 6分
又
¼¼¼¼¼ 7分
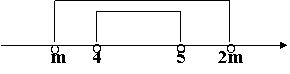∴当
时，
，此时＝
当
时，
，此时＝
当
时，
，此时＝
¼¼¼¼¼ 9分
要(A∩B)C，即要：（4，5）C，
∴必须要有：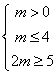
¼¼¼¼¼12分
故所求的范围为 
¼¼¼¼¼ 13分
22、解：①∵对于任意的（0，＋∞）都有，
∴
＝
¼¼¼¼¼ 3分
有＝1，∴＝3。
¼¼¼¼¼ 4分
②又
＝
＝
¼¼¼¼¼ 6分
所以原不等式可化为：＜，
¼¼¼¼¼ 8分
又在定义域（0，＋∞）上为增函数，∴
¼¼¼¼¼10分
所以根据定义域和单调性有：
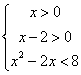
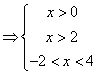
¼¼¼¼¼ 13分
故不等式的解集为：
。
¼¼¼¼¼ 14分