高一向量练习
班级 学号 姓名
一．选择题：
1．设
是正
的中心，则向量
，
，
是
(
)平行向量
(
)相等向量
(
)模相等的向量
(
)有相同的起点的向量
2．下列命题正确的是
()模为
的向量与任一向量平行 ()共线向量都相等
()单位向量都相等
()平行向量不一定是共线向量
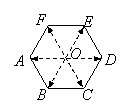3．
是正六边形，是中心，则图中与向量相等的向量为
()
()
()
()
4．下列各等式或不等式中，一定不能成立的个数是
①
②
③
④
()
()
()
()
5．已知正方形
的边长为，
，
，
，则
的模等于
()
()
()
()
6．在平行四边形中，
为
上任一点，则
等于
()
()
()
()
7．是四边形对角线的交点，
，
，
，
，则
成立的充要条件是四边形是
()等腰梯形 ()平行四边形 ()菱形
()矩形
8．下面给出四个命题：
①
对于实数
和向量
、
，恒有
；
② 对于实数、
和向量，恒有
；
③ 若
，则
；
④ 若
，则
.
其中正确的命题个数是
() () ()
()
9．若是平行四边形对角线的交点，
，
，则
等于
() () 
() 
() 
10．设
、
是不共线的两个向量，则向量
与向量
共线的充要条件是
() 
()
()
()
11．设四边形，有
，且
，则这个四边形是
()平行四边形
()矩形
()等腰梯形 ()菱形
12．如图，已知
，
，
，
，且四边形为平行四边形，则
()
()
()
()
13．若是的重心，则下列各向量中与共线的是
()
()
()
()
14．已知
，
，
，则下列关系一定成立的是
()，，三点共线
()，，三点共线
()，，三点共线
()，，三点共线
请将选择题的答案填在下面的表格中：
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 答 案 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
二．填空题：
15．
是
的 （填充分不必要、必要不充分、充要、既不充分也不必要）条件。
．设 ，为非零向量，若
，则的方向与的方向
．
．向量，满足
，
，则
的最大值和最小值分别是
．
．在中，点，
，
分别是
，
，
的中点，
则
．
．设命题
：向量与共线，命题
：有且只有一个实数
，使得
，
则是的
条件。
．化简：
．
三．解答题：解答应写出文字说明、证明过程或演算步骤。
．若
，化简
．
．、分别为凸四边形的对角线
、
的中点，
，
，
用、表示向量
．
．设两个非零向量
和
不共线，
（1）如果
，
，
，求证：，，共线；
（2）试确定实数
的值，使
和
共线。
24．一架飞机从地按北偏西
的方向飞行
到达地，然后向地飞行，设 地恰在地的北偏东，并且
两地相距，求飞机从地向地飞行的方向和
两地的距离。
25．设
是三边上的点，它们使
，若
，试用
将
表示出来。