高一应用数学竞赛辅导训练
1.若集合M＝｛x,y,z｝，集合N＝｛3，0，－3｝，f是从M到N的映射，则满足f(x)+f(y)+f(z)=0的映射有
(A)6个 (B)7个 (C)8个 (D)9个
2．某商品降价10%后，欲恢复原价，则应提价（ ）。
（A）10% （B）9%
（C）11% （D）11
%
3．某工厂去年12月的月产值是a，已知月平均增长率为p，则今年12月产值比去年同期增加的倍数是（ ）。
（A）(1＋p)12－1 （B）(1＋p)12 （C）(1＋p)11 （D）1
4．某人从1993年起，每年7月1日到银行存入a元一年定期存款，若年利率为r保持不变，且每年存款到期后，原存款和利息自动转存为新的一年定期，到2000年7月1日将所有存款和利息全部取回，他可取回的钱数是（ ）。
（A）a(1＋r)6
（B）a(1＋r)7 （C）a(1＋r)8 （D）a
5．某林场原有森林木材存量为a，木材的每年增长率为25%，而每年冬天要砍伐的木材量为x，为了实现经过20年达到木材存有量至少翻两翻的目标，则x的最大值是（ ）。(计算时取lg2=0.3)
（A）
a （B）
a （C）
a （D）
a
6．某商品分两次提价，有三种提价方案，方案甲：第一次提价p%，第二次提价q%；方案乙：第一次提价q%，第二次提价p%；方案丙：第一次提价
%，第二次提价%，已知p>q>0，则上述三个方案中（ ）。
（A）方案甲提价较多 （B）方案乙提价较多
（C）方案丙提价较多 （D）以上都不对
7．某商场出售一种商品，每天可卖1000件，每件可获利4元，根据经验，若每件少卖1角钱，则每天可多卖出100件，为获得最好的经济效益，每件单价应比现在减少（ ）。
（A）1.5元 （B）2元 （C）3元 （D）2.5元
8．A处存放电线杆40根，现要从离A相距1000米的B处起，在线段AB的延长线上，每隔50米架设电线杆一根，一辆汽车每次能运4根，全部运到后又返回A处运第二车，…，问40根电线杆全部到位后，汽车再返回A地待命，其总路程为（ ）。
（A）40千米 （B）41千米 （C）42千米 （D）40.5千米
9.无盖的圆柱形容器的底面半径为
，母线为3，现将盛水的该容器平稳地缓慢倾斜，当水剩到原来的
时，圆柱的母线与水平面所成的角α∈（ ）
(A)（0，
） (B)（，
） (C)（，
） (D)（，
）
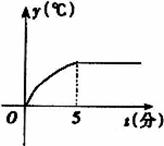10.在某种金属材料的耐高温实验中，温度随着时间变化的情况由微机记录后显示出的图象如右图所示，现给出下面说法 ①前5分钟温度增加的速度越来越快
②前5分钟温度增加的速度越来越慢 ③5分钟以后温度保持匀速增加 ④5分钟以后温度保持不变。其中正确的说法是
(Ａ)①与④ (B)②与④ (C)②与③ (D)①与③
11．在一次足球预选赛中，某小组共有5个球队进行又循环赛（每两队之间赛两场），已知胜一场得3分，平一场得1分，负一场得0分.积分多的前两名可出线（积分相等则要比净胜球数或进球总数）.赛完后一个队的积分可出现的不同情况种数为 （ ）
A．22 B．23 C．24 D．25
12．有一件商品的成本为1000元，若在月初出售，可获利100元，然后将本利存入银行(已知银行月息为2%)；若在下月初出售，可获利120元，但要付5元保管费，则
(Ａ)本月初出售获利大 (C)在本月初出售和在下月初出售获利相同
(B)在下月初出售获利大 (D)在本月初出售和在下月初出售获利大小不能确定
13．某种电热水器的水箱盛满水是200升，加热到一定温度，即可浴用，浴用时，已知每分钟放水34升，在放水的同时按
毫升／秒2的匀加速自动注水(即t分钟自动注水2t2升).当水箱内的水量达到最小值时，放水程度自动停止，现假定每人洗浴用水量为65升，则该热水器一次至多可供
(A)3人洗浴 (B)4人洗浴 (C)5人洗浴 (D)6人洗浴
14．在一定的条件下，某种细胞经过1小时1个分裂为2个，已知一定数量的细胞经过20个小时的分裂，细胞的个数成为230个，那么分裂到215个细胞需要
(A)1.6小时 (B)5小时 (C)2小时 (D)1.5小时
15．4个茶杯和5包茶叶的价格之和小于22元，而6个茶杯与3包茶叶的价格之和大于24元，则2个茶杯和3包茶叶的价格比较
(A)2个茶杯贵 (B)3包茶叶贵 (C)相同 (D)无法确定
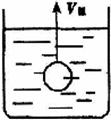16．如图，在一个盛了水的圆柱形容器内，其水面以下有一个用细线吊着的下端开了很小的孔、充满水的薄壁小球，当慢慢地匀速地将小球从水下向水面以上拉动时，柱形容器内水面的高度h与时间t的函数图象大致是
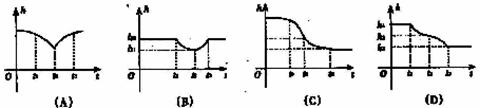
17．某公司从2000年起，每人的年工资由三个项目组成并按下表规定实施
| 项目 | 计算办法 |
| 基础工资 | 2000年1万元，考虑物价因素，以后每年递增10% |
| 住房补贴 | 按工龄计算：400元×工龄(工龄计算方法，如某职工1998年进公司，到2001年按4年计算) |
| 医疗费 | 每年1600元，固定不变 |
该公司的一职工在2002年将得到的住房补贴和医疗费之和可超过基础工资的25%，这位职工的工龄至少是
(A)2年 (B)3年 (C)4年 (D)5年
18．有一块长方形的窗台，尺寸为1米×0.2米，现有足够多规格相同的白色壁砖和蓝色壁砖（规模为0.2米×0.2米），用这些整块壁砖贴满窗台（空隙忽略不计），可以贴成_________种不同图案。
19．容器A中盛有浓度为a的盐水6升，容器B中盛有浓度为b的盐水4升，现将A中溶液1升倒入B，混合后，再从B中倒1升入A，这样反复k次(由A倒入B，再由B倒入A算一次)后，A、B中盐水的浓度分别为a k, b k, 则b k－a k的表达式为 。
| 20．某工程有右图所示的工序组成，那么工程所需的最短时间是 天。 | 工 序 | a | b | c | d | e |
| 前道工序 | － | a | a | b | c,d | |
| 工时数(天) | 2 | 3 | 5 | 6 | 3 |
21. 某工程的工序流程图如下(工时数单位：天)：
则工程所需的最短时间
天。
22．有一游泳池长50ｍ，甲在游泳时经测算发现，他每游10ｓ，速度减慢0．2ｍ／ｓ，已知他游完50ｍ全程的时间是38ｓ，则他入水时的游泳速度是 .
23．在一支长15厘米，粗细均匀的圆柱形蜡烛的下端固定一个薄金属片(体积不计)，使蜡烛恰好能竖直地浮于水中，上端有1厘米高的部分露在水面上，已知蜡烛比重为0.85克／立方厘米，现在点燃蜡烛，当蜡烛被水淹没时，它的剩余长度是 .
24． 在半径为30米的圆形广场中央上空，设置一个照明光源，射向地面的光是圆锥形，且其轴截面顶角为120°，若要光源恰好照亮整个广场，则其高度应
为 米。
25． 如图所示的几何体是从一个圆柱中挖去一个以圆柱的上底面为面，下底面圆心为顶点的圆锥而得到的，现用一个平面去截这个几何体，若这个平面垂直于圆柱底面所在的平面，那么所截得的图形可能是图中的_________.（把所有可能的图的序号都填上）。
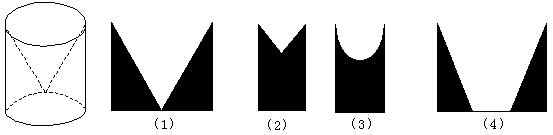
26. 一位商人有一种货，如果月初售出可获利100元，再将本利存入银行，已知银行月息为2.4%，如果月末售出可获利120元，但要付保管费5元，问这种货是月初售出好，还是月末售出好？
27. 铁道机车运行1小时所需的成本由两部分组成：固定部分m元，变动部分与运行速度V(千米/小时)的平方成正比，比例系数为k(k>0)，如果机车匀速从甲站开往乙站，为了使成本最省，应以怎样的速度运行？
28. 某渔场养的鱼，第一年鱼的重量增长率200%，以后每年的重量增长率都是前一年的一半，(I) 当饲养4年后，鱼的重量是原来的多少倍？(II) 如果由于某种原因每年损失预计重量的10%，那么经过多少年后，鱼的总重量开始减少？
29. 为了保护环境，实现城市绿化，某房地产公司要在拆迁地长方形ABCD上规划出一块长方形地面建造住宅小区公园(公园的一边落在CD上)，但不跨越文物保护区△AEF的红线EF，问如何设计才能使公园占地面积最大？并求出最大面积。（已知AB＝CD＝200m，BC＝AD＝160m，AE＝40m，AF＝60m）
30. 某工厂今年1月、2月、3月生产的某种产品的数量分别为1万件，1.2万件，1.3万件，为了估计以后每个月的产量，以这三个月的产品数量为依据，用一个函数模拟该产品的月产量y与月份x的关系，模拟函数可用二次函数或y=a·bx＋c (a, b, c为常数)，已知四月份产品的产量为1.37万件，请问用以上哪个函数作为模拟函数较好，说明理由，并写出这个函数。
31. 某市镇1997年底人口为5.0万人，人口年平均增长率为0.01，如果每年住房面积增加4000平方米，那么到2005年底人均住房面积仅能维持原有水平，为了使到2005年底人均住房面积比1997年底增加10%，需要每年住房面积增加多少平方米？
32.
生产某种商品x吨，所需费用为(
x2＋5x＋1000)元，而售出x吨这种商品时，每吨售价为p元，这里p依关系式p=a＋
(a, b为常数)而定，（I）写出这种商品所获得的利润y元与售出这种商品的吨数x的函数关系式；（II）如果生产出来的这种商品都能卖完，那么当产量是150吨时所获利润最大，并且这时每吨的售价为40元，求a, b的值。
33.
某河流一段区域，汛前的水位为120cm，水位警戒线高为300cm，水位超过警戒线时，河坝就会发生危险，预测汛期来临时，水位线的提高量Ln与汛期天数n的函数关系为Ln=20
，为防止河坝发生危险，堤坝上有泄水涵道，每天泄水量可使水位线下降40cm，如果从汛期来临的第一天起，就开始泄水排洪，试问从第几天起河坝会出现险情？
34.
某企业在“减员增效”中，对部分人员实行分流，规定分流人员第一年可以到原单位领取工资的100%，从第二年起，以后每年只能在原单位按上一年的
领取工资。该企业根据分流人员的技术特长，计划创办新的经济实体，该实体预计，第一年属投资阶段没有利润，第二年每人可获得b元收入，从第三年起，每人收入可在上一年的基础上递增50%。如果某人分流前每年收入为a元，分流后第n年收入为a n元，（I）求a n；（II）当b=
a时,这个人哪一年收入最少？最少是多少元？（III）当b≥
a时，是否可以保证这个人分流一年后的年收入永远超过分流前的年收入？
35. 某企业经过调整后，第一年资金增长率为300%，以后每年的增长率都是前一年增长率的
，（I）经过4年后，企业资金是原资金的多少倍？（II）若由于某种原因每年损失资金的5%，那么经过多少年后，企业的资金开始下降？
36. 甲、乙两地相距40公里，某人以每小时V公里的速度骑车由甲赴乙，到达乙后，他以原速度返回，行至某处，因故停留了20分钟，停留后他以比原速度每小时快4公里的速度继续前进，若他由乙地返回甲地的的归途中所用的时间不比从甲地到乙地所用的时间多，求V的取值范围。
37. 某公司生产一种产品，每年需投入固定成本0.5万元，此外每生产100件这种产品还需投资2.5万元，经预测知市场对这种产品的年需求量为500件，且当售出这种产品的数量为t(单位：百件)时，销售所得收入约为5t－
万元，（I）若该公司这种产品的年产量为x(单位：百件, x>0)，试把该公司生产销售这种产品的年利润表示为当年产量x的函数；
（II）当该公司的年产量多大时，当年所得利润最大，
（III）当该公司的年产量多大时，当年不会亏本？
38. 有甲、乙两个粮食经销商，每次同时、同地、同价格购进粮食(随市场调节，每次粮价可能不同)，它们各购粮3次，甲每次购粮10000kg，乙每次购粮用10000元，规定谁平均每千克支付的粮款少，谁的购粮方式就更经济，试判断甲、乙两人谁的购粮方式更经济？并证明你的结论。
39 、我国是水资源比较贫乏的国家之一，各地采用价格调控手段来达到节约用水的目的.某市用水收费的方法是：水费＝基本费+超额费+损耗费.若每月用水量不超过最低限量a m3时，只付基本费8元和每户每月定额损耗费c元，若用水量超过a m3时，除了付同上的基本费和损耗费外，超过部分每m3付b元的超额费.已知每户每月的定额损耗费不超过5元.
该市一家庭今年第一季度的用水量和支付费用如表所示：
| 月 份 | 用水量 | 水 费 |
| 1月 | 9m3 | 9元 |
| 2月 | 15m3 | 19元 |
| 3月 | 22m3 | 33元 |
试根据上面表格中的数据求a、b、c.
40．开始时，烧瓶里有N个细菌，每小时末，细菌的数量和这一小时初的细菌数量相比增加10%，除此以外，在每小时末，从烧瓶里取出含有n个细菌的一份，问经过n小时后，烧瓶里的细菌的数量(取出相应的份数后)就超过开始时细菌数量的一倍?并确定有解的条件．
41．某厂使用两种零件A、B装配两种产品P、Q，该厂的生产能力是月产P最多2500件，月产Q最多1200件.而组装一件P需4个A，2个B；组装一件Q需6个A，8个B.某个月该厂能用的A最多有14000个，B最多有12000个.已知产品P每件利润1000元，Q每件利润2000元，欲使该月利润最高，需组装P、Q产品各多少件?最高利润多少万元?
42．机动车过大桥，为了安全，同一股道上的两辆车的间距不得小于kLV 2，其中V千米/小时是车速，L(米)是平均车身长度，k为比例系数，经测定：车速为60千米/小时，安全车距1044L米.
(Ⅰ)规定怎样的车速可使同一股道上的车流量最大?(车流量即单位时间内通过的车辆数)；
(Ⅱ)设过桥的车辆平均身长为5米，求同一股道上每小时最大流量.
43．这是一个计算机程序的操作说明：
（1）初始值x=1，y=1，z=0，n=0；
（2）n=n+1（将当前n+1的值赋予新的n）；
（3）x=x+2（将当前x+2的值赋予新的x）；
（4）y=2y（将当前2y的值赋予新的y）；
（5）z=z+xy（将当前z+xy的值赋予新的z）；
（6）如果z＞7000，则执行语句（7），否则回语句（2）继续进行；
（7）打印n，z；
（8）程序终止.
由语句（7）打印出的数值为 ， .
以下写出计算过程：
44．现有流量均为300ｍ3／s的两条河流A、B，汇合于某处后，不断混合，它们的含沙量分别为2kg／ｍ3和0．2kg／ｍ3，假若从汇合处开始，沿岸设有若干个观测点，两股水流在汇经相邻两个观测点的过程中，其混合效果相当于两股水流在1秒钟内交流100ｍ3的水量，即从A股流入B股100ｍ3水，经混合后，又从B股流入A股100ｍ3水并混合. (Ⅰ)问从第几个观测点开始，两股河水的含沙量之差小于0．01kg／ｍ3，(不考虑沙沉淀)；
(Ⅱ)随着两股水流的不断混合，它们的含沙量趋向于一个常数，试求出这个常数.
45．近几年来，沙尘暴肆虐我国西北地区，造成了严重的自然灾害，因此，在今后若干年内防沙治沙已成为沙漠地区一项重要而又艰巨的工作。某县位于沙漠边缘地带，人与自然经过长期顽强的斗争，到2000年底全县绿化率已达30%，但每年的治沙工作都出现这样的情形：上一年的沙漠面积的16%被栽上树改造为绿洲，而同时，上一年的绿洲面积的4%又被侵蚀，变为沙漠，设该县的土地面积为1，第一年（即2000年）底的绿洲面积为a1，第二年底的绿洲面积为a2，…，第n年底的绿洲面积为an.
（1）试找出an与an－1的递推关系，并写成“
”的形式；
（2）至少要到哪一年底，该县的绿洲面积才能超过60%？
到2003年底，该县的绿洲面积能否达到或超过50%？
46．运输一批海鲜，可在汽车、火车、飞机三种运输工具中选择，它们的速度分别为50千米/小时，100千米/小时，500千米/小时，每千米的运费分别为a元、b元、c元，且b＜a＜c，又这批海鲜在运输过程中的损耗为500元/小时，若使用三种运输工具分别运输时各自的总费用（运费与损耗之和）互不相等，试确定使用哪种运输工具总费用最省。（题中字母均为正的已知量）
47．某公司生产的A型商品通过租赁柜台进入某商场销售.第一年，商 场为吸引厂家，决定免收该年管理费，因此，该年A型商品定价为每件70元，销售量为11.8万件.第二年，商场开始对该商品征收比率为p%的管理费（即每销售100元要征收p 元），于是该商品的定价上升为每件
元，预计年销售量将减少p万件.
（1）将第二年商场对商品征收的管理费y（万元）表示成p的函数，并指出这个函数的定义域；
（2）要使第二年商场在此项经营中收取的管理费不少于14万元，则商场对该商品征收管理费的比率p%的范围是多少？
（3）第二年，商场在所收费不少于14万元的前提下，要让厂家获得最大销售金额，则p应为多少？
高一应用数学辅导训练参考答案
3．32种。
4．①③。
6．解：（1）依题意，第二年该商品年销量为（11.8-p），年销售收入为
，则
商场该年对该商品征收的总管理费为
p%（万元）.
故所求函数为：
…4分 由11.8－p>0及p>0
得定义域为
（2）由
,得
化简，得
解得
，故当比率在[2%，10%]内时，商场收取的管理费将不少于14万元.
（3）第二年，当商场收取的管理费不少于14万元时，厂家的销售收入为
为减函数，
∴g（p）max=g（2）=700（万元）故当比率为2%时，厂家销售金额最大，且商场所收管理费又不少于14万元.
提示：(1)据物理知识：小孔很小，所以拉出水面时，小球下孔流出的水在水的表面张力下呈油面，使水不能从小孔流出，所以小球是带着一腔水被拉出的．
(2)据数学知识，由球顶到球中心被拉出时，水面高度下降得快，所以曲线向下凸；当球从中心开始到整个球被拉出时，水面高度下降得慢，所以曲线向上凸，但在球顶拉出水面到球被安全拉出水面的过程中，水面均下降，所以函数在此过程中是减函数．
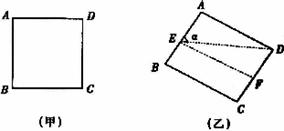提示：如图是容器的轴截面，图(甲)是倒水前的，图(乙)是倒水后的，由题意知AE＝2，α＝∠AED，tgα＝ 
，由tg 
(1)B
提示：满足3+0+(-3)=0有 
＝6个；满足0＋0＋0＝0有1个，由加法原理共有
6＋1＝7个.
(9)A
提示：设一个茶杯和一包茶叶的价格分别为x,y元，则有 
由②得2x+y＞8 ③
由③得－4x－2ｙ＜－16 ④
①＋④得3ｙ＜6
由③得－10x－5ｙ＜－40 ⑤
①＋⑤得2x＞6，故选A
(15)6 
厘米
设蜡烛横截面积为S(平方厘米)，金属片重a克，则依题意有15×Ｓ×0．85＋ａ＝14×Ｓ×1又设当水面以上的1厘米长蜡烧完后，蜡烛上升了x厘米．
则有14×Ｓ×0．85＋ａ＝（14－ｘ）×Ｓ×1
从二式消去a，得x=0.85(厘米)
同样推理，当水面以上这0．85厘米蜡烛烧完后，可算出蜡烛又上升了0.852／厘米，
如此继续下去，燃烧的各段蜡烛长度的和是1+0．85＋0．852＋…＝ 
解：设r＝1＋10％＝1．1，那么取出相应的份数以后，烧瓶里的细菌的个数是：
第一小时末：N·ｒ－n
第二小时末：(Nr-n)·ｒ-n＝Ｎ·ｒ2-n·ｒ－n
……
第t小时末：N·ｒｔ－n·ｒｔ－1－n·ｒｔ－2－…－n·ｒ－n
＝Ｎ·ｒｔ－ 
由已知得N·ｒｔ－ ＞2Ｎ
解之得rｔ＞ 
（当N(r-1)-n＞0时）
即1．1ｔ＞ 
∴ｔ＞ 
当N＞10n时，问题有解．
(6)Ｂ提示：观察直线的图象变化率，选Ｂ．
(21)设每月用水量为ｘｍ3，支付费用为ｙ元，则
由题意知0＜ｃ≤5，∴8＋ｃ≤13
由表中数据知2、3月份的费用均大于13元，故用水量15ｍ3，22ｍ3均大于最低限量ａｍ3，将ｘ＝15，ｘ＝22分别代入得：
∴ｂ＝2，2ａ＝ｃ＋19 ③
再分析1月份的用水量是否超过最低限量，不妨设9＞ａ，将ｘ＝9代入②得，9＝8＋2（9－ａ）＋ｃ，即2ａ＝ｃ＋1７，这与③矛盾.
∴9≤ａ，1月份的付款方式应选①式，
则8＋ｃ＝9，ｃ＝1，
故ａ＝10，ｂ＝2，ｃ＝1
（12）B
提示：水箱在t分钟后的水量f（ｔ）＝2ｔ2－34ｔ＋200＝2（ｔ－
）2＋ 
．
∴f（ｔ）ｍiｎ＝55．5
水箱从200升水降到这个值，用了 分钟，放出34× ＝289(升)，
由
知，一次至多可供4人洗浴.
(13)1．6ｍ／ｓ
提示：由ｖ×10＋（ｖ－0．2）×10＋（ｖ－0．4）×10＋（ｖ－0．6）×8＝50 
ｖ＝1．6（ｍ／ｓ）
(21)设分别生产P、Q产品x件、y件，则0≤x≤2500，0≤y≤1200，
依题意，4x＋6y≤14000，2x＋8y≤12000，
即2x＋3y≤７000，x＋4y≤6000（1）
该月产品利润为1000x＋2000y＝1000（x＋2y）
欲使利润最大，可先求在(1)的条件下，x+2y的最大值.
设x+2y=u(2x+3y)+v(x+4y)，
则
于是，
当且仅当
即
时上式取等号
此时最高利润为1000×（x＋2y）＝400(万元)
答：组装P产品2000件，Q产品1000件时，该月利润最高，为400万元.
(5)B
220x＝230
设原有细胞x个，则
2ax＝215
220－a＝215，a＝5.
(8)C
提示：2002年的基础工资1×1.12＝1.21（万元），设工龄为x年，则400x+1600＞12100×25％，解之得x＞3.5625.
由于工龄取整数即得x≥4.
(21)设安全车距为d米，车流量为Q辆/小时
由V＝60，d＝1.44L得k= 
∵Ｑ＝ 
（Ⅰ）仅当kV＝ 
，即V=50千米/小时，车流量最大
(Ⅱ)当L＝5(米)时，每小时最大车流量为500辆.
(20)(Ⅰ)设含沙量为akg／ｍ3，bkg／ｍ3的两股水流在单位时间内流过的水量分别为ｐｍ3，ｑｍ3，则根据化学知识，其混合后的含沙量为kg／ｍ3，又设第n个观测点处A股水流含沙量为ankg／ｍ3，B股水流含沙量为bnkg／ｍ3，(n∈N)
则a1＝2，b1＝0．2
即
∴ 
①
②
由①－②得 
即数列（an－bn）是以1.8为首项， 
为公比的等比数列
∴ 
由已知an－bn＜0．01 
2n－1＞180
∴n≥9
即从第9个观测点开始，两股水流的含沙量之差小于0．01kg／ｍ3．
(Ⅱ)由①＋②得：an＋bn＝an－1＋bn－1
即｛an＋bn｝是常数列，∴an＋bn＝2．2 ④
由③＋④得 
∴ 
即两股水流含沙量最终趋向于一个常数，这个常数为1．1kg／ｍ3．
21．（1）
…………………………4分（文科6分）
（2）（理）由（1）知
又
是公比为
的等比数列……6分 
………8分
若
即 
为减函数.∴n－1≥5 即n≥6………11分
故至少要到2005年底，该县的绿洲面积才能超过60%.………………………………………………11分
（文）由已知
.从而……………………7分 
.
………10分 故到2003年底，该县的绿洲面积能超过50%……………12分
3.答案：D
提示：到1994年7月1日，可取a(1＋r), 到1995年7月1日可取a(1＋r)2＋(1＋r), ……,到2000年7月1日可取a(1＋r)7＋a(1＋r)6＋……＋a(1＋r)＝a
4.答案：C
提示：a1=a, a2=
a－x, a n=a n－1－x, a n－a n－1=(a n－1－a n－2)=(a2－a1)()n－1, 依次代入得a21=a1＋4×(
－x)[()20－1], 要求a21≥4a, 解得x≤a
1、答案：D
提示：设原价为a，降价后为0.9a,
设提价为x，则0.9a(1＋x)=a, x=11%
5.答案：C
提示：方案甲：(1＋p%)(1＋q%); 方案乙：(1＋q%)(1＋p%); 方案丙：(1＋%)(1＋%)=1＋(p＋q)%＋(%)2>(1＋p%)(1＋q%), ∴方案丙提价较多
6.答案：A
提示：设减少x角，则效益y=(40－x)(1000＋100x)=100(－x2＋30x＋400), 当x=15时, y取得最大值，∴每件单价应比现在减少1.5元
7.答案：B
提示：第一次运4根，返回时行程为2×1150=2300, 第二次行程为2700，共10次，总行程为
×10×(2300＋5900)=41000
8.答案：10
米
提示：30×ctg60°=10
9.答案：(b－a)()n
提示：b1=
, a1=
, ……，∴b n=
, a n=
, ∴bn－a n=(b n－1－a n－1), ∴{ bn－a n }是以b－a为首项，为公比的等比数列，b k－a k＝(b－a)()n
10.答案：当成本费大于525元时，月初售出好，当成本费小于525元时，月末售出好
提示：设成本费为x元，若月初售出，到月末共获利100＋(x＋100)×2.4%元, 若月末售出可获利115元，比较得[100＋(x＋100)×2.4%]－115＝2.4%(x－525), ∴当成本费大于525元时，月初售出好，当成本费小于525元时，月末售出好
11.答案：V=
提示：设1小时成本为m＋kV2元, 又设甲、乙两站间的距离为S千米，需运行
小时, 总成本y=(m＋kV2)=S(
＋kV)≥2S
, 当＝kV时，等号成立，此时V=
答案：(I) 11
倍；(II) 经过5年，鱼的重量开始减少
提示：（I）设鱼原来的重量为a，过n年后的重量为a n，a1=2a, a2=3a(1＋1)=6a, a3=6a(1＋)=9a, a4=9a(1＋)=11a, (II)
由a n=a n－1(1＋
), 且每年损失预计重量的10%, 若an≥an＋1, 得a n≥an(1＋
)×90%, ∴2n－1≥9, n≥5, ∴经过5年，鱼的重量开始减少
13.答案：当P点到AD的距离等于10m时，面积最大，最大面积大约是24067(m2)
提示：设P点到BC的距离为PH＝x， 则由相似三角形的性质得PG＝120＋(200－x), ∴矩形PHCG的面积是S=x[120＋(200－x)]=－x2＋
x=－(x－190)2＋×1902, 当x=190时, Smax=×1902
24067
14.答案：指数函数y=－0.8·(0.5)x＋1.4
提示：设函数为y=a·bx＋c, 将x=1, y=1; x=2,
y=1.2; x=3, y=1.3,分别代入得ab＋c＝1，ab2＋c=1.2, ab3＋c=1.3, 解得a=0.8, b=0.5,
c=1.4, ∴函数为y=－0.8·(0.5)x＋1.4, 将x=4代入得y1.37
15.答案：9200平方米
提示：设1997年底人均住房面积为a, 到2005年人口总数为5(1＋0.01)8, 则5 a (1＋0.01)8=5a＋3.2, 又设需要为达到人均住房面积比1997年底增加10%的目标，每年住房面积增加x平方米，则5 a (1＋0.01)8(1＋10%)=5a＋8x, 其中5a=
, 代入解得x=
0.92, ∴需要每年住房面积增加9200平方米
16.答案：(I) y=(
－)x2＋(a－5)x－1000 ; (II) a=45, b=－30
提示：(I) y=x(a＋
)－(x2＋5x＋100)= (－)x2＋(a－5)x－1000 ; (II) 当x=150时, p=40, a＋
=40, =
, 且二次函数取得最大值，∴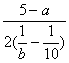 
=150, 联立解得a=45, b=－30
17.答案：第28天
提示：设x天可能出现险情，则120＋20－40n>300, >9＋12n, 解得n>27或n<－3(舍去)，∴第28天会出现险情
18.答案：(I) a n=a()n－1＋b(
)n－2 ； (II) 第三年最少，为
a； (III) 可以保证
提示：(I) c1=a, c2=a, ……,c n=()n－1a, b1=0,
b2=b, b3=b(1＋),……,
bn=b(1＋)n－2, ∴两数列相加得a1=a, a2=a＋b, ……,a n= a()n－1＋b()n－2,
(II) b=a时, a n= a()n－1＋a()n－5≥2a
=a,
当n=3时,等号成立，
(III) 若b≥a, 则an≥a()n－1＋a()n－2≥2a
=a,
∴可以保证这个人分流一年后的年收入永远超过分流前的年收入
19.答案：(I) 
a, (II) 5年
提示：(I) 设该企业原来的资金为a，则第一年后为4a, 第二年后为4a(1＋100%)=8a, 第三年后为
a, 第四年后为a,
(II) 按以上规律知a n＋1=a n[1＋3×()n]×0.95≤a n, 解得()n≤
, n≥4, ∴n＋1=5, 经过5年企业资金开始下降
20.答案：V∈(0, 20)
提示：设某人在距甲地S公里处M点停留，则M到乙地的距离是40－S，
∴
≥
＋
＋, 其中0<S<40,
整理得－－≥0,
∴V2＋4V－12S≤0, ∴－2－2
≤V≤－2＋2， 0<S<40,
∴将 S＝0与S＝40分别代入得0<V<20
21.答案：（I）y=－x2＋
x－ (II)
x=2.5 （III）0.21≤x≤4.79
提示：(I) 该公司这种产品的年产量为x, 利润y=5x－
－－x =－x2＋x－, 0≤x≤5
(II) y=－(x－)2＋
, ∴当x=2.5时, 当年利润最大,
(III) －x2＋x－≥0, 
≤x≤
, ∴0.21≤x≤4.79
22.答案：乙的购粮方式更经济
提示：设三次的粮价分别是a1, a2, a3, 则甲的平均购粮价为
≥
, 乙的平均购粮价为
≤
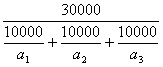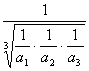=, ∴乙的购粮方式更经济
23.答案：14天
24.答案：11天