高中一年级数学第二学期期末考试试卷
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1页至第2页,第Ⅱ卷第3页至第6页,全卷满分150分,考试时间120分钟。
第Ⅰ卷 (选择题 满分60分)
注意事项:
1.答第Ⅰ卷前,请考生将自己的姓名、准考证号、考试科目用2B铅笔填涂在答题卡上;
2.每小题选出答案后,用铅笔把答题卡上对应题号的大难标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上;
3.考试结束后,将第Ⅱ卷和答题卡一并收回。
一.选择题:本大共12小题,每小题5分,在每小题的四个选项中只有一个是正确的.
1、时钟的分针经过40分钟时间旋转的角度是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、半径为3的圆中有一条弧的长度是![]() ,则此弧所对的圆周角是( )
,则此弧所对的圆周角是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、若![]() ,
,![]() ,
,![]() ,则
,则![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、下列函数中,周期为1的奇函数是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、若![]() 、
、![]() 、
、![]() 为任意向量,
为任意向量,![]() ,则下列等式不一定成立的是( )
,则下列等式不一定成立的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
6、函数![]() 的图象的一个对称中心的坐标是( )
的图象的一个对称中心的坐标是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、设![]() 、
、![]() 、
、![]() 是任意的非零向量,且相互不共线,给出下列三个命题:①
是任意的非零向量,且相互不共线,给出下列三个命题:① ![]() ;
;
② ![]() 不与
不与![]() 垂直; ③
垂直; ③ ![]()
其中真命题的个数是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8、已知![]() ,
,![]() ,则下列不等关系中必定成立的是( )
,则下列不等关系中必定成立的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、已知![]() ,且
,且![]() 为锐角,则
为锐角,则![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、已知平面上四个互异的点A、B、C、D满足:![]() ,
,
则![]() 的形状是( )
的形状是( )
A、等边三角形 B、等腰三角形 C、直角三角形 D、斜三角形
11、已知关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有解,则实数
内有解,则实数![]() 的取值范围是( )
的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、将函数![]() 的图象按向量
的图象按向量![]() 平移后得到函数
平移后得到函数![]() 的图象,给出以下四个结论:① 可取
的图象,给出以下四个结论:① 可取![]() ;② 可取
;② 可取![]() ;③ 可取
;③ 可取![]() 或
或![]() ;④ 可取无数个
;④ 可取无数个![]() ;其中正确的是( )
;其中正确的是( )
A、① B、① ② C、① ② ③ D、① ② ③ ④
 高中一年级第二学期期末考试试卷
高中一年级第二学期期末考试试卷
数 学 答 题 卷
一.选择题:本大共12小题,每小题5分,在每小题的四个选项中只有一个是正确的.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
第Ⅱ卷 (非选择题 共90分)
二.填空题:本大题共4个小题,每小题4分,共16分,把答案直接添在题中的横线上。
13、已知![]() ,
,![]() ,若单位向量
,若单位向量![]() 与
与![]() 同向,则向量
同向,则向量![]() 的坐标是______________.
的坐标是______________.
14、计算:![]() ,其值为 ___________________.
,其值为 ___________________.
15、函数![]() 的图象按向量
的图象按向量![]() 平移后,图象的解析式是______________.
平移后,图象的解析式是______________.
16、观察![]() ;
;![]() ;
;
请写出一个与以上两式规律相同的等式:__________________________________.
三.解答题: 本大题共6个小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本题满分12分)
在直角坐标系![]() 中,已知点
中,已知点![]() 和点
和点![]() ,其中
,其中![]() ,若向量
,若向量![]() 与
与![]() 垂直,求
垂直,求![]() 的值。
的值。
18.(本题满分12分)
已知![]() ,函数
,函数![]()
(1)求![]() 的值;(2)若
的值;(2)若![]() 表示
表示![]() 在
在![]() 上的反函数,试求
上的反函数,试求![]() 的值。
的值。
19.(本题满分12分)
在![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 的对边长,已知
的对边长,已知![]() 、
、![]() 、
、![]() 成等比数列,
成等比数列,
且![]()
求:(1)角![]() 的值; (2)
的值; (2)
![]() 的值。
的值。
20.(本题满分12分)
设向量![]() ,
,![]() ,
,![]()
![]() 。
。
(1)求![]() ; (2)求
; (2)求![]() 的模的最小值。
的模的最小值。
21.(本题满分12分)
已知某海滨浴场的海浪高度![]() (米)是时间
(米)是时间![]() (
(![]() ,单位:小时)的函数,记作:
,单位:小时)的函数,记作:![]() ,下表是某日各时的浪高数据:
,下表是某日各时的浪高数据:
|
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
|
| 1.5 | 1.0 | 0.5 | 1.0 | 1.49 | 1 | 0.51 | 0.99 | 1.5 |
经长期观察,![]() 的曲线可近似地看成函数
的曲线可近似地看成函数![]()
![]()
![]() 的图象。
的图象。
(1)根据以上数据,求出函数![]()
![]() 的函数表达式;
的函数表达式;
(2)依据规定,当海浪高于1米时才对冲浪爱海好者开发,请依据(1)的结论,判断一天内的上午8:00至20:00之间,有多少时间可供冲浪爱好者进行运动。
 22.(本题满分14分)
22.(本题满分14分)
设![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,![]() ;当
;当![]() 时,有
时,有![]()
![]() ,
,
求:(1)![]() 关于
关于![]() 的表达式;
的表达式;
(2)![]() 的值
的值
(3)函数![]() 的单调递增区间。
的单调递增区间。
高中一年级第二学期期末考试试卷
数 学 参 考 答 案
一.选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | C | C | D | A | C | D | C | B | A | D |
1、解:![]()
2、解:![]() 圆周角为
圆周角为![]()
3、解:![]() ,
,![]() ,
,![]()
![]()
4、解:![]() ,但为偶函数;
,但为偶函数;![]() 非奇函数;
非奇函数;![]() ,且为奇函数 ;
,且为奇函数 ;![]()
5、解:由向量的数量积不满足结合律得:![]() 不一定成立
不一定成立
6、解:由![]() 的对称中心为
的对称中心为![]()
![]() 知:代入使
知:代入使![]() 的值为
的值为![]() 整数倍的成立
整数倍的成立
7、解:因![]() 、
、![]() 、
、![]() 是任意的非零向量,且相互不共线,则由三角形三边关系得①
是任意的非零向量,且相互不共线,则由三角形三边关系得①![]() 成立;②取
成立;②取![]() =
=![]() =
=![]() =
=![]() ,则 由
,则 由![]() 知
知![]() 不与
不与![]() 垂直不成立; ③ 由向量运算知:
垂直不成立; ③ 由向量运算知:![]() 成立
成立
8、解:由![]() ;
;![]() 得:
得:![]() 第一象限
第一象限
![]()
![]() 成立
成立
9、解:![]()
10、解:![]()
![]() 以AB、AC为边的平行四边形为菱形
以AB、AC为边的平行四边形为菱形![]() AB=AC
AB=AC![]()
![]() 为等腰三角形
为等腰三角形
11、解: ![]()
![]() ,又∵
,又∵![]() ∴
∴![]() ∴
∴![]()
代![]() 成立,代
成立,代![]() 成立,从而选A
成立,从而选A
12、解:将函数![]() 图象上任意点
图象上任意点![]() 按向量
按向量![]() 平移后得到函数
平移后得到函数![]() 图象上对应点
图象上对应点![]() ,则:
,则:![]() ① 及
① 及![]() ,代入
,代入![]() 得
得![]() ,即
,即![]() ② ,对比①②得
② ,对比①②得![]() ,故:
,故:![]() ,从而应选D
,从而应选D
二.填空题:
13、![]() 解:
解:![]() ,
,![]()
![]()
与![]() 同向的单位向量
同向的单位向量![]()
14、![]() 解:
解: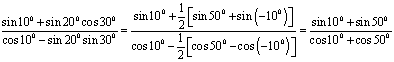
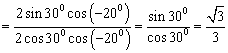
15、![]() 按向量
按向量![]() 平移后得
平移后得![]() ,即
,即![]()
16、解:![]()
![]() ;
;
观察得规律:化为正弦后两角和为![]() 即可;
即可;
如:![]()
三.解答题:
17.解: ∵![]() ,
,![]()
∴![]() ,
,![]()
又∵![]() ∴
∴![]()
即:![]()
![]()
![]() ,
, ![]() ,
,![]() 或
或![]()
又∵![]() ∴
∴![]()
18.解1:(1)∵![]() ∴
∴![]()
又∵![]() ∴
∴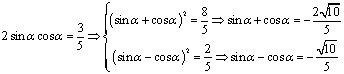
∴两式相加得:![]()
(2)∵![]()
![]()
即![]()
又由(1)得:![]() ∴
∴![]()
∴当![]() 时有
时有![]()
又∵![]() ∴
∴![]() ∴由反函数性质得:
∴由反函数性质得:![]()
解2:(1)∵![]() ∴
∴![]()
又∵![]() ∴
∴![]()
又∵![]() ∴
∴![]()
(2)∵![]()
![]()
即![]()
设![]() ,则
,则![]()
∴![]() ,
,![]()
∴![]() 故:
故:![]()
∴![]()
19.解:(1)∵![]() 、
、![]() 、
、![]() 成等比数列 ∴
成等比数列 ∴![]()
又∵![]() ∴
∴![]()
又∵![]() ∴
∴![]()
![]()
又∵![]() ∴
∴![]()
(2)∵由![]() 知:
知:![]() ∴
∴![]()
又∵由![]() 知:
知:![]() ∴
∴![]()
20.解:(1)∵![]() ,
,![]()
∴![]()
![]()
(2)∵![]()
∴![]()
![]()
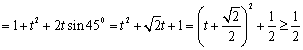 ∴
∴![]()
故:![]() 的模的最小值为
的模的最小值为![]() ,此时
,此时![]()
21.解:(1)依题意得: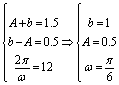 ∴
∴![]() 的表达式为:
的表达式为:![]()
(2)![]() 得:
得:![]()
∵![]()
![]() ;
;![]()
![]()
又∵![]() ∴
∴![]()
∴![]()
![]()
故:一天内的上午8:00至20:00之间,有6时间可供冲浪爱好者进行运动。
22.解:(1)![]()
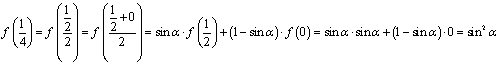
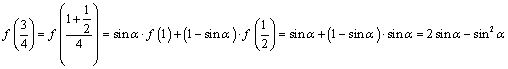
(2)由![]()
![]() 得:
得: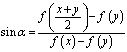
取![]() ,则:
,则:
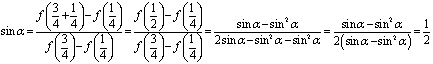
又∵![]() ∴
∴![]()
(3)∵![]()
∴当![]()
![]() ,
,
即![]()
![]() 时,函数单调递增
时,函数单调递增
故:![]() 的单调递增区间为:
的单调递增区间为:![]()
![]()