函数y=Asin(ωχ＋φ)的图象习题精选

函数y=Asin(ωχ＋φ)的图象习题精选

一、选择题

1．下列命题中正确的是（　　　）

　　A．将 的图像沿 轴向右平移 个单位，得到 的图像

　　B．函数 的图像，当 时由 的图像向右平移 个单位得到

　　C． 的图像可由 的图像上所有点的纵坐标不变，横坐标缩小为原来的 倍得到

　　D． 的图像可由 的图像上各点横坐标不变，纵坐标缩小为原来的 倍得到

2．函数 的图像可以由函数 的图像经过下列哪种变换得到（　　　）

　　A．向右平移 个单位　　　　　　　  B．向右平移 个单位

　　C．向左平移 个单位　　　　　　　  D．向左平移 个单位

3．在 上既是增函数，又是奇函数的是（　　　）

　　A． 　　　　　　　　  B．

　　C． 　　　　　　　　  D．

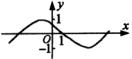
5．右图是周期为 的三角函数 的图像，那么 可以写成（　　　）

　　A． 　 　　　　 B．

　　C． 　　　　　　 D．

6．函数 的图像的一条对称轴方程是（　　　）

　　A． 　　　 B． 　　　 C． 　　　　D．

7．已知 ， ，则 的图像（　　　）

　　A．与 的图像相同 

　　B．与 的图像关于 轴对称

　　C．向左平 个单位，得到 的图像

　　D．向右平移 个单位，得到 的图像

8．函数 的图像关于原点中心对称的充要条件是（　　 ）

　　A．　　　　B． （ ）

　　C． （ ）　　　　D． （ ）

9．正弦函数 的定义域为 ，周期为 ，初相为 ，值域为［－1，3］，则其函数式的最简形式为（　　  ）

　　A． 　　　　 　B．

　　C． 　　　　 D．

10．函数 的周期为2（其中 ），则 为（　　　）

　　A．　　B．　　C．　　D．

11．函数 的单调增区间为（　　　）

　　A． （ ）

　　B． （ ）

　　C． （ ）

　　 D． （ ）

12．函数 （ ）在区间［a，b］上是增函数，且 ， ，则函数 在［a，b］上（　　 ）

　　A．是增函数　　　　　　　　　　  B．是减函数

　　C．可以取得最大值 　　　　　　 D．可以取得最小值

二、填空题

　　13．正弦函数 的定义域为 ，周期为 ，初相为 ，值域为［－1，3］，则 ．

　　14．函数 ，当 时，取最小值．

　　15．将函数 的图像上各点向右平移 个单位，再把横坐标缩小到原来的一半，然后把纵坐标伸长到原来的5倍，最后把整个图像向下平移4个单位，则所得图像的解析式为_____________．

　　16．关于函数 （ ），有下列命题

　　①由 可得 必是 的整数倍；

　　② 的表达式可改写成 ；

　　③ 的图像关于点 对称；

　　④ 的图像关于直线 对称．

　　其中正确命题的序号为___________．

三、解答题

　　17．求函数 的单调区间．

　　18．已知函数 （ ， ， ）的最大值为4，最小值为0，最小正周期为 ，其图像的一条对称轴为 ．求该函数的解析式．

　　19．如图，某地一天从6时至14时的温度变化曲线近似满足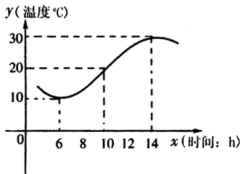函数．

　　（1）求这段时间的最大温差；

　　（2）写出这段曲线的函数解析式．

　　20．已知函数 ．

　　（1）用“五点法”作函数图像；

　　（2）说出此图像与正弦曲线 之间的关系；

　　（3）求函数的周期、振幅、初相；

　　（4）指出函数的单调区间．

　　21．受日月引力，海水会发生涨落，这种现象叫做潮汐．在通常情况下，船在涨潮时驶进航道，靠近船坞；卸货后落潮时返回海洋．某港口水的深度 （米）是时间 （ ，单位：时）的函数，记作 ，下面是该港口在某季节每天水深的数据：

（时）	0	3	6	9	12	15	18	21	24
（米）	10.0	13.0	9.9	7.0	10.0	13.0	10.1	7.0	10.0

　　经长期观察， 曲线可以近似地看做函数 的图像．

　　（1）根据以上数据，求出函数 的近似表达式．

　　（2）一般情况下，船舶航行时，船底离海底的距离为5米或5米以上时认为是安全的（船舶停靠时，船底只需不碰海底即可），某船吃水深度（船底离水面的距离）为6.5米．如果该船想在同一天内安全进出港，问它至多能在港内停留多长时间（忽略进出港所需的时间）？

参考答案：

一、选择题

　　1．C　2．B　3．D　5．D  6．A　7．D　8．B　9．A　10．A　11．C　12．C

二、填空题

　　13． 　 14． （ ）

　　15． 　

　　16．②、③

三、解答题

　　17．它的减区间即函数 的增区间，由 ，得 （ ），即减区间为 （ ），同样可求增区间为 （ ）．

　　18．由题意 ， ，∴ ， ．

　　又 ，∴ ，∴ ．

　　∵ 是它的一条对称轴，∴ ，

　　∴ （ ）．

　　从而 （ ）．

　　∵ ，∴ 或 ．

　　故该函数的解析式为 ， ．

　　19．（1）由题中图所示，这段时间的最大温差是30－10＝20（℃）

　　（2）图中从6时到14时的图像是函数 的半个周期的图像，∴ ，解得 ．

　　由图示， ， ．

　　这时 ．将 ， 代入上式，可得 ．

　　综上，所求解析式为 ， ．

　　20． ，

　　（1）由 、 、 、 、 求出 、 、 、 、 ．（可以看到0、 、 、 、 间隔 、 、 、 、 、 间隔 ，所以不需要解五个方程分别求 ．）

	0
	0		0		0

　　在同一坐标系中，作出 、 、 、 、 五个点，并用光滑曲线连接起来．

　　（2）∵ ，

　　∴首先将 ， 的图像所有点向右平移 个单位；再把所得的图像上各点的横坐标缩短到原来的 倍（纵坐标不变）；最后把所得的图像上所有点的纵坐标伸长到原来的 倍（横坐标不变），从而得到 ， 的图像，这就是此函数的图像与正弦曲线之间的关系．

　　（3）周期 （也可以依据公式 ， 来求）；振幅 ；依定义 叫相位， 时的 叫做初相，所以初相应该是 ．

　　（4）由 ，

　　得 ， ．

　　由 ，

　　得 ， ．

　　∴原函数单调增区间为 ， ；

　　单调减区间为 ， ．

　　21．（1）由数据知函数 的周期 ，振幅 ， ， ．

　　（2）由题意，该船进出港时，水深应不小于5＋6.5＝11.5米．

　　 ， ， （ ）， （ ）．

　　在同一天内，取 或1， 或，

　　∴该船最早能在凌晨1时进港，下午17时出港，在港口最多停留16小时．